Dictionary as a string

The simplest data structure for the dictionary is to sort the vocabulary lexicographically and store it in an array of fixed-width entries as shown in Figure 5.3 . Assuming a Unicode representation, we allocate $2\times 20$We allocate 20 bytes for the term itself (because few terms have more than twenty characters in English), 4 bytes for its document frequency, and 4 bytes for the pointer to its postings list. Four-byte pointers resolve a 4 gigabytes (GB) address space. For large collections like the web, we need to allocate more bytes per pointer. We look up terms in the array by binary search.

For Reuters-RCV1, we need $M \times (2 \times 20+4+4) = 400{,}000 \times 48 = 19.2 \mbox{ megabytes (MB)}$ $M \times (20+4+4) = 400{,}000 \times 28 = 11.2 \mbox{megabytes (MB)}$ for storing the dictionary in this scheme.

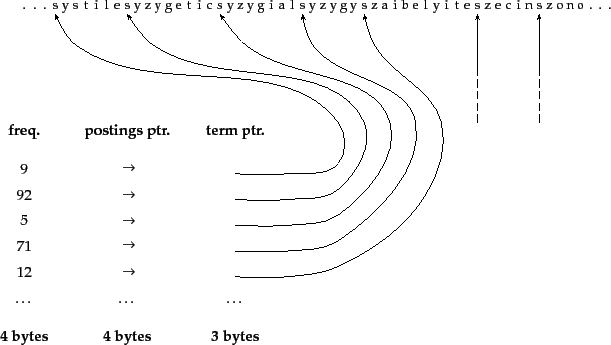Dictionary-as-a-string storage.Pointers mark the end of the preceding term and the beginning of the next. For example, the first three terms in this example are systile, syzygetic, and syzygial.

Using fixed-width entries for terms is clearly wasteful. The average length of a term in English is about eight characters icompresstb1, so on average we are wasting twelve characters (or 24 bytes) in the fixed-width scheme. Also, we have no way of storing terms with more than twenty characters like hydrochlorofluorocarbons and supercalifragilisticexpialidocious. We can overcome these shortcomings by storing the dictionary terms as one long string of characters, as shown in Figure 5.4 . The pointer to the next term is also used to demarcate the end of the current term. As before, we locate terms in the data structure by way of binary search in the (now smaller) table. This scheme saves us 60% compared to fixed-width storage - 24 bytes on average of the 40 bytes 12 bytes on average of the 20 bytes we allocated for terms before. However, we now also need to store term pointers. The term pointers resolve $400{,}000 \times 8 = 3.2 \times 10^6$ positions, so they need to be $\log_2 3.2 \times 10^6 \approx 22$ bits or 3 bytes long.

In this new scheme, we need $400{,}000 \times (4+4+3+\unicode{2\times}{} 8) = \unicode{10.8}{7.6} \ \mbox{MB}$ for the Reuters-RCV1 dictionary: 4 bytes each for frequency and postings pointer, 3 bytes for the term pointer, and $\unicode{2\times}{} 8$ bytes on average for the term. So we have reduced the space requirements by one third from 19.211.2 to 10.87.6 MB.

Blocked storage with four terms per block.The first block consists of systile, syzygetic, syzygial, and syzygy with lengths of seven, nine, eight, and six characters, respectively. Each term is preceded by a byte encoding its length that indicates how many bytes to skip to reach subsequent terms.