![\includegraphics[totalheight=3in]{PrecisionRecall.eps}](img532.png) |
Precision, recall, and the F measure are set-based measures. They are
computed using unordered sets of documents. We need to extend these
measures (or to define new measures) if we are to evaluate the ranked
retrieval results that are now standard with search engines.
In a ranked retrieval context, appropriate sets of retrieved documents are
naturally given by the top ![]() retrieved documents. For each such set,
precision and recall values can
be plotted to give a precision-recall curve , such as the one shown
in Figure 8.2 . Precision-recall curves have a
distinctive saw-tooth shape: if the
retrieved documents. For each such set,
precision and recall values can
be plotted to give a precision-recall curve , such as the one shown
in Figure 8.2 . Precision-recall curves have a
distinctive saw-tooth shape: if the ![]() document retrieved is nonrelevant then recall is the same as for the top
document retrieved is nonrelevant then recall is the same as for the top
![]() documents, but precision has dropped. If it is relevant, then both
precision and recall increase, and the curve jags up and to the right.
It is often useful to remove these jiggles and the standard way to do
this is with an interpolated precision: the interpolated precision
documents, but precision has dropped. If it is relevant, then both
precision and recall increase, and the curve jags up and to the right.
It is often useful to remove these jiggles and the standard way to do
this is with an interpolated precision: the interpolated precision
![]() at a certain
recall level
at a certain
recall level ![]() is defined as the highest precision found for any recall
level
is defined as the highest precision found for any recall
level ![]() :
:
| (42) |
The justification is that almost anyone would be prepared to look at a few more documents if it would increase the percentage of the viewed set that were relevant (that is, if the precision of the larger set is higher). Interpolated precision is shown by a thinner line in Figure 8.2 . With this definition, the interpolated precision at a recall of 0 is well-defined (Exercise 8.4 ).
| Recall | Interp. |
| Precision | |
| 0.0 | 1.00 |
| 0.1 | 0.67 |
| 0.2 | 0.63 |
| 0.3 | 0.55 |
| 0.4 | 0.45 |
| 0.5 | 0.41 |
| 0.6 | 0.36 |
| 0.7 | 0.29 |
| 0.8 | 0.13 |
| 0.9 | 0.10 |
| 1.0 | 0.08 |
Examining the entire precision-recall curve is very informative, but there is often a desire to boil this information down to a few numbers, or perhaps even a single number. The traditional way of doing this (used for instance in the first 8 TREC Ad Hoc evaluations) is the 11-point interpolated average precision . For each information need, the interpolated precision is measured at the 11 recall levels of 0.0, 0.1, 0.2, ..., 1.0. For the precision-recall curve in Figure 8.2 , these 11 values are shown in Table 8.1 . For each recall level, we then calculate the arithmetic mean of the interpolated precision at that recall level for each information need in the test collection. A composite precision-recall curve showing 11 points can then be graphed. Figure 8.3 shows an example graph of such results from a representative good system at TREC 8.
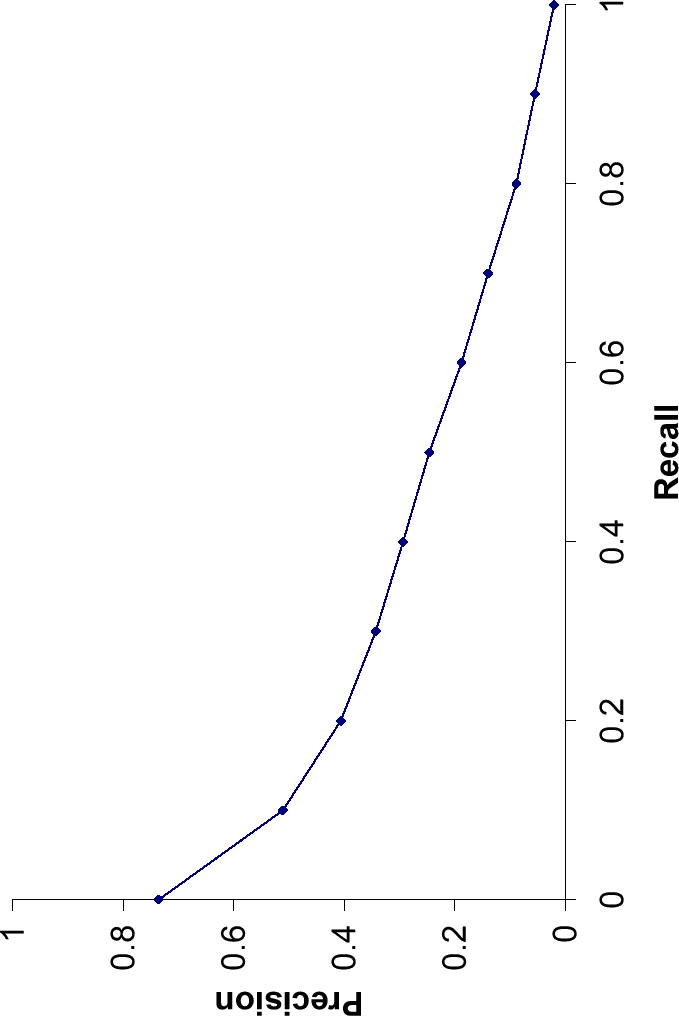 Averaged 11-point precision/recall graph across 50 queries for
a representative TREC system.The Mean Average Precision for this system is
0.2553.
Averaged 11-point precision/recall graph across 50 queries for
a representative TREC system.The Mean Average Precision for this system is
0.2553.
In recent years, other measures have become more common. Most
standard among the TREC community is
Mean Average Precision
(MAP), which provides a single-figure measure of quality across recall
levels. Among evaluation measures, MAP has been shown to have
especially good discrimination and stability.
For a single information need, Average Precision is the average of the precision
value obtained for the set of top
![]() documents existing after each relevant document is retrieved, and this value is then averaged over information needs.
That is, if the set of relevant documents for an information need
documents existing after each relevant document is retrieved, and this value is then averaged over information needs.
That is, if the set of relevant documents for an information need ![]() is
is
![]() and
and
![]() is the set of ranked retrieval results from the top result until
you get to document
is the set of ranked retrieval results from the top result until
you get to document ![]() , then
, then
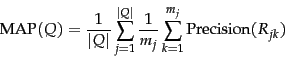 |
(43) |
Using MAP, fixed recall levels are not chosen, and there is no interpolation. The MAP value for a test collection is the arithmetic mean of average precision values for individual information needs. (This has the effect of weighting each information need equally in the final reported number, even if many documents are relevant to some queries whereas very few are relevant to other queries.) Calculated MAP scores normally vary widely across information needs when measured within a single system, for instance, between 0.1 and 0.7. Indeed, there is normally more agreement in MAP for an individual information need across systems than for MAP scores for different information needs for the same system. This means that a set of test information needs must be large and diverse enough to be representative of system effectiveness across different queries.
The
above measures factor in precision at all recall levels.
For many prominent applications, particularly web search,
this may not be germane to users. What matters is
rather how many good results there are on the first page or
the first three pages. This leads to measuring precision at
fixed low levels of retrieved results, such as 10 or 30
documents. This is referred to as ``Precision at ![]() '', for
example ``Precision at 10''. It has the advantage of not
requiring any estimate of the size of the set of relevant
documents but the disadvantages that it is the least stable of the
commonly used evaluation measures and that it does not average
well, since the total number of relevant documents for a
query has a strong influence on precision at
'', for
example ``Precision at 10''. It has the advantage of not
requiring any estimate of the size of the set of relevant
documents but the disadvantages that it is the least stable of the
commonly used evaluation measures and that it does not average
well, since the total number of relevant documents for a
query has a strong influence on precision at ![]() .
.
An alternative, which alleviates this problem, is R-precision .
It requires having a set of known
relevant documents ![]() , from which we calculate the
precision of the top
, from which we calculate the
precision of the top ![]() documents returned.
(The set
documents returned.
(The set ![]() may be incomplete, such as when
may be incomplete, such as when ![]() is formed by
creating relevance judgments for the pooled top
is formed by
creating relevance judgments for the pooled top ![]() results of
particular systems in a set of experiments.)
R-precision adjusts for the size
of the set of relevant documents: A perfect system could score
1 on this metric for each query, whereas, even a perfect system could
only achieve a precision at 20 of 0.4 if there were only 8
documents in the collection relevant to an information need.
Averaging this measure across queries thus makes more sense. This measure
is harder to explain to naive users than Precision at
results of
particular systems in a set of experiments.)
R-precision adjusts for the size
of the set of relevant documents: A perfect system could score
1 on this metric for each query, whereas, even a perfect system could
only achieve a precision at 20 of 0.4 if there were only 8
documents in the collection relevant to an information need.
Averaging this measure across queries thus makes more sense. This measure
is harder to explain to naive users than Precision at ![]() but easier to explain than MAP.
If there are
but easier to explain than MAP.
If there are ![]() relevant documents for a query, we examine the top
relevant documents for a query, we examine the top
![]() results of a system, and find that
results of a system, and find that ![]() are relevant, then by
definition, not only is the precision (and hence R-precision)
are relevant, then by
definition, not only is the precision (and hence R-precision) ![]() ,
but the recall of this result set is also
,
but the recall of this result set is also ![]() . Thus, R-precision
turns out to be identical to the
break-even point , another measure
which is sometimes used, defined in terms of this equality relationship holding.
Like Precision at
. Thus, R-precision
turns out to be identical to the
break-even point , another measure
which is sometimes used, defined in terms of this equality relationship holding.
Like Precision at ![]() , R-precision describes only one point on
the precision-recall curve, rather than attempting to summarize
effectiveness across the curve, and it is somewhat unclear why you should
be interested in the break-even point rather than either the best point on the curve (the
point with maximal F-measure) or a retrieval level of interest to a particular application (Precision at
, R-precision describes only one point on
the precision-recall curve, rather than attempting to summarize
effectiveness across the curve, and it is somewhat unclear why you should
be interested in the break-even point rather than either the best point on the curve (the
point with maximal F-measure) or a retrieval level of interest to a particular application (Precision at ![]() ). Nevertheless, R-precision turns out to be highly correlated with MAP empirically, despite measuring only a single point on the curve.
). Nevertheless, R-precision turns out to be highly correlated with MAP empirically, despite measuring only a single point on the curve.
Another concept sometimes used in evaluation is an ROC curve .
(``ROC'' stands for ``Receiver Operating
Characteristics'', but knowing that doesn't help most people.)
An ROC curve plots the true positive rate or sensitivity against the
false positive rate or (
![]() ). Here,
sensitivity is just another term for recall.
The false positive rate is given by
). Here,
sensitivity is just another term for recall.
The false positive rate is given by ![]() .
Figure 8.4 shows the ROC curve
corresponding to the precision-recall curve in
Figure 8.2 . An ROC curve always goes from the bottom
left to the top right of the graph. For a good system, the graph climbs
steeply on the left side.
For unranked result sets, specificity , given by
.
Figure 8.4 shows the ROC curve
corresponding to the precision-recall curve in
Figure 8.2 . An ROC curve always goes from the bottom
left to the top right of the graph. For a good system, the graph climbs
steeply on the left side.
For unranked result sets, specificity , given by ![]() ,
was not seen as a very useful notion. Because the set
of true negatives is always so large, its
value would be almost 1 for all information needs (and,
correspondingly, the value of
the false positive rate would be almost 0). That is, the
``interesting'' part of Figure 8.2 is
,
was not seen as a very useful notion. Because the set
of true negatives is always so large, its
value would be almost 1 for all information needs (and,
correspondingly, the value of
the false positive rate would be almost 0). That is, the
``interesting'' part of Figure 8.2 is
![]() , a part which is compressed to a small
corner of Figure 8.4 . But an ROC curve could make sense when
looking over the full retrieval spectrum, and it provides another way of
looking at the data.
In many fields, a common aggregate measure is to report
the area under the ROC curve, which is the ROC analog of MAP.
Precision-recall curves
are sometimes loosely referred to as ROC curves. This is
understandable, but not accurate.
, a part which is compressed to a small
corner of Figure 8.4 . But an ROC curve could make sense when
looking over the full retrieval spectrum, and it provides another way of
looking at the data.
In many fields, a common aggregate measure is to report
the area under the ROC curve, which is the ROC analog of MAP.
Precision-recall curves
are sometimes loosely referred to as ROC curves. This is
understandable, but not accurate.
A final approach that has seen increasing adoption,
especially when employed with machine learning approaches to
ranking svm-ranking is measures of
cumulative gain , and in particular normalized
discounted cumulative gain ( NDCG ). NDCG is
designed for situations of non-binary notions of relevance
(cf. Section 8.5.1 ). Like precision at ![]() , it is
evaluated over some number
, it is
evaluated over some number ![]() of top search results. For a set of
queries
of top search results. For a set of
queries ![]() , let
, let
![]() be the relevance score assessors gave to document
be the relevance score assessors gave to document
![]() for query
for query ![]() . Then,
. Then,
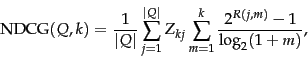 |
(44) |
Exercises.
| (45) |
System 1 R N R N N N N N R R System 2 N R N N R R R N N N
R R N N N N N N R N R N N N R N N N N R