 |
The premier venue
for research on XML retrieval
is the INEX (INitiative
for the Evaluation of XML retrieval) program, a
collaborative effort that has produced reference collections,
sets of queries, and relevance judgments. A yearly INEX
meeting is held to
present and discuss research results.
The INEX 2002 collection consisted of about 12,000 articles from
IEEE journals. We give collection statistics in
Table 10.2 and show
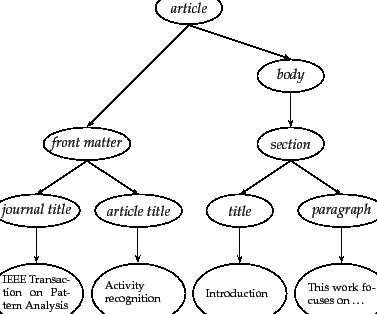
part of the schema of the collection in
Figure 10.11 . The IEEE journal collection was expanded
in 2005. Since 2006 INEX uses the much larger English
Wikipedia as a test collection. The relevance of
documents is judged by human assessors using the methodology introduced in
Section 8.1 (page ![]() ), appropriately modified for structured documents
as we will discuss shortly.
), appropriately modified for structured documents
as we will discuss shortly.
Two types of information needs or in INEX are content-only or CO topics and content-and-structure (CAS) topics. CO topics are regular keyword queries as in unstructured information retrieval. CAS topics have structural constraints in addition to keywords. We already encountered an example of a CAS topic in Figure 10.3 . The keywords in this case are summer and holidays and the structural constraints specify that the keywords occur in a section that in turn is part of an article and that this article has an embedded year attribute with value 2001 or 2002.
Since CAS queries have both structural and content criteria, relevance assessments are more complicated than in unstructured retrieval. INEX 2002 defined component coverage and topical relevance as orthogonal dimensions of relevance. The component coverage dimension evaluates whether the element retrieved is ``structurally'' correct, i.e., neither too low nor too high in the tree. We distinguish four cases:
The topical relevance dimension also has four levels: highly relevant (3), fairly relevant (2), marginally relevant (1) and nonrelevant (0). Components are judged on both dimensions and the judgments are then combined into a digit-letter code. 2S is a fairly relevant component that is too small and 3E is a highly relevant component that has exact coverage. In theory, there are 16 combinations of coverage and relevance, but many cannot occur. For example, a nonrelevant component cannot have exact coverage, so the combination 3N is not possible.
The relevance-coverage combinations are quantized
as follows:
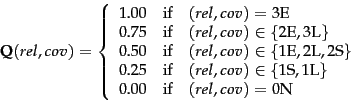 |
(54) |
The number of relevant components in a retrieved set ![]() of
components can
then be computed as:
of
components can
then be computed as:
| (55) |
One flaw of measuring relevance this way is that overlap is
not accounted for. We discussed the concept of marginal
relevance in the context of unstructured retrieval in
Section 8.5.1 (page ![]() ). This problem is worse in XML retrieval
because of the problem of multiple nested elements occurring
in a search result as we discussed on
page 10.2 .
Much of the recent focus at
INEX has been on developing algorithms and evaluation
measures that return non-redundant results lists and evaluate
them properly. See the references in Section 10.6 .
). This problem is worse in XML retrieval
because of the problem of multiple nested elements occurring
in a search result as we discussed on
page 10.2 .
Much of the recent focus at
INEX has been on developing algorithms and evaluation
measures that return non-redundant results lists and evaluate
them properly. See the references in Section 10.6 .
|
Table 10.3 shows two INEX 2002 runs of the vector space system we described in Section 10.3 . The better run is the SIMMERGE run, which incorporates few structural constraints and mostly relies on keyword matching. SIMMERGE's median average precision (where the median is with respect to average precision numbers over topics) is only 0.147. Effectiveness in XML retrieval is often lower than in unstructured retrieval since XML retrieval is harder. Instead of just finding a document, we have to find the subpart of a document that is most relevant to the query. Also, XML retrieval effectiveness - when evaluated as described here - can be lower than unstructured retrieval effectiveness on a standard evaluation because graded judgments lower measured performance. Consider a system that returns a document with graded relevance 0.6 and binary relevance 1 at the top of the retrieved list. Then, interpolated precision at 0.00 recall (cf. page 8.4 ) is 1.0 on a binary evaluation, but can be as low as 0.6 on a graded evaluation.
|
Table 10.3 gives us a sense of the typical
performance of XML retrieval, but it does not
compare structured with unstructured retrieval.
Table 10.4 directly shows the effect of using
structure in retrieval. The results are for a
language-model-based system (cf. Chapter 12 ) that is
evaluated on a subset of CAS topics from INEX 2003 and
2004. The evaluation metric is precision at ![]() as defined
in Chapter 8 (page 8.4 ). The
discretization function used for the evaluation maps
highly relevant elements
(roughly corresponding to the 3E elements defined for
Q) to 1
and all other elements to 0. The content-only
system treats queries and documents as unstructured bags of
words. The full-structure model ranks elements that satisfy
structural constraints higher than elements that do not. For
instance, for the query in Figure 10.3 an element
that contains the phrase summer holidays in a section
will be rated higher than one that contains it in an
abstract.
as defined
in Chapter 8 (page 8.4 ). The
discretization function used for the evaluation maps
highly relevant elements
(roughly corresponding to the 3E elements defined for
Q) to 1
and all other elements to 0. The content-only
system treats queries and documents as unstructured bags of
words. The full-structure model ranks elements that satisfy
structural constraints higher than elements that do not. For
instance, for the query in Figure 10.3 an element
that contains the phrase summer holidays in a section
will be rated higher than one that contains it in an
abstract.
The table shows that structure helps increase precision at
the top of the results list. There is a large increase of
precision at ![]() and at
and at ![]() . There is almost no improvement
at
. There is almost no improvement
at ![]() .
These results demonstrate the benefits of structured retrieval.
Structured retrieval imposes
additional constraints on what to return and documents that
pass the structural filter are more likely to be relevant.
Recall may suffer because some
relevant documents will be filtered out, but for
precision-oriented tasks structured retrieval is superior.
.
These results demonstrate the benefits of structured retrieval.
Structured retrieval imposes
additional constraints on what to return and documents that
pass the structural filter are more likely to be relevant.
Recall may suffer because some
relevant documents will be filtered out, but for
precision-oriented tasks structured retrieval is superior.