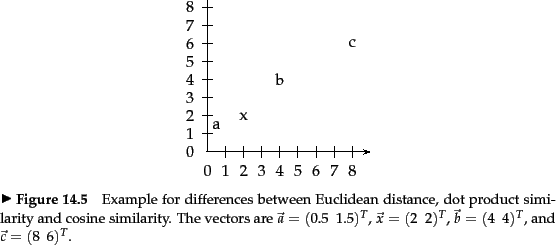Next: Support vector machines and
Up: Vector space classification
Previous: References and further reading
Contents
Index
Exercises.
- In Figure 14.13 , which of the three
vectors
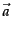 ,
, 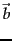 , and
, and 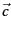 is (i)
most similar to
is (i)
most similar to 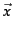 according to dot product similarity,
(ii) most similar to
according to dot product similarity,
(ii) most similar to 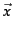 according to cosine similarity,
(iii) closest to
according to cosine similarity,
(iii) closest to 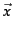 according to Euclidean distance?
according to Euclidean distance?
-
Download Reuters-21578 and train and test Rocchio
and kNN classifiers for the classes
acquisitions,
corn,
crude,
earn,
grain,
interest,
money-fx,
ship,
trade, and
wheat.
Use the ModApte split.
You may want to use one of a number of software packages that
implement Rocchio classification and kNN classification, for
example, the Bow toolkit (McCallum, 1996).
- Download 20 Newgroups (page 8.2 ) and train and test Rocchio
and kNN classifiers for its 20 classes.
- Show that the decision boundaries in Rocchio
classification are, as in kNN, given by the Voronoi tessellation.
- Computing the distance between a dense centroid
and a sparse vector is
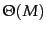 for a naive implementation
that iterates over all
for a naive implementation
that iterates over all 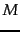 dimensions. Based on the equality
dimensions. Based on the equality
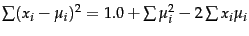 and assuming that
and assuming that 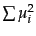 has been precomputed,
write down an algorithm that is
has been precomputed,
write down an algorithm that is
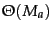 instead, where
instead, where
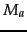 is the number of distinct terms in the test document.
is the number of distinct terms in the test document.
- Prove that the region of the plane consisting of all points
with the same
 nearest neighbors is a convex polygon.
nearest neighbors is a convex polygon.
-
Design an algorithm that performs an efficient 1NN search in
1 dimension (where efficiency is with respect to the number
of documents
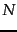 ). What is the time complexity of the algorithm?
). What is the time complexity of the algorithm?
- Design an algorithm that performs an efficient 1NN search in
2 dimensions with at most polynomial (in
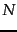 ) preprocessing time.
) preprocessing time.
- Can one design an exact efficient algorithm for
1NN for very large
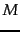 along the ideas you used to solve the
last exercise?
along the ideas you used to solve the
last exercise?
-
Show that
Equation 145 defines a hyperplane
with
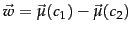 and
and
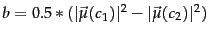 .
.
Figure 14.14:
A simple non-separable set of points.
|
- We can easily construct non-separable data sets in high
dimensions by embedding a non-separable set like the one
shown in Figure 14.14 .
Consider embedding Figure 14.14 in 3D and then perturbing the
4 points slightly (i.e., moving them a small
distance in a random direction).
Why would you expect the resulting
configuration to
be linearly separable?
How likely is then a non-separable set of
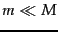 points
in
points
in 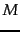 -dimensional space?
-dimensional space?
-
Assuming two classes, show that the percentage of
non-separable assignments of the vertices of a hypercube
decreases with dimensionality
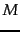 for
for 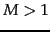 . For example,
for
. For example,
for 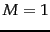 the proportion of non-separable assignments is 0,
for
the proportion of non-separable assignments is 0,
for 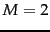 , it is
, it is 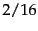 . One of the two non-separable cases
for
. One of the two non-separable cases
for 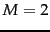 is shown in
Figure 14.14 , the other is its mirror image. Solve
the exercise either analytically or by simulation.
is shown in
Figure 14.14 , the other is its mirror image. Solve
the exercise either analytically or by simulation.
- Although we point out the similarities of Naive Bayes
with linear vector space classifiers, it does not make
sense to represent count vectors (the document
representations in NB) in a continuous vector
space. There is however a formalization of NB that is
analogous to Rocchio. Show that NB assigns a document to the
class (represented as a parameter vector) whose
Kullback-Leibler (KL) divergence
(Section 12.4 , page 12.4 )
to the document (represented as a count
vector as in Section 13.4.1 (page
![[*]](http://nlp.stanford.edu/IR-book/html/icons/crossref.png) ), normalized to sum to 1) is
smallest.
), normalized to sum to 1) is
smallest.





Next: Support vector machines and
Up: Vector space classification
Previous: References and further reading
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07