




Next: Feature selectionChi2 Feature selection
Up: Feature selection
Previous: Feature selection
Contents
Index
Mutual
information
A common feature selection method is to compute 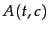 as
the expected mutual information (MI) of term
as
the expected mutual information (MI) of term 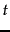 and
class
and
class 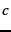 .
.![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png) MI measures how much information the
presence/absence of a term contributes to making the correct
classification decision on
MI measures how much information the
presence/absence of a term contributes to making the correct
classification decision on 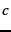 . Formally:
. Formally:
where 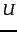 is a random variable that
takes values
is a random variable that
takes values 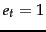 (the document contains term
(the document contains term 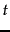 ) and
) and
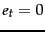 (the document does not contain
(the document does not contain 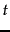 ),
as defined on page 13.4 , and
),
as defined on page 13.4 , and 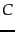 is a random variable
that takes values
is a random variable
that takes values 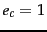 (the document is in class
(the document is in class 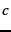 ) and
) and 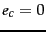 (the document is not in
class
(the document is not in
class 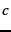 ).
We write
).
We write 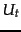 and
and 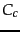 if it is not clear from context which term
if it is not clear from context which term 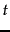 and class
and class 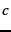 we are referring to.
we are referring to.
For
MLEs of the probabilities,
Equation 130 is equivalent to Equation 131:
where the 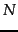 s are
counts of documents that have the values of
s are
counts of documents that have the values of
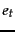 and
and 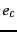 that are indicated by the two subscripts.
For example,
that are indicated by the two subscripts.
For example,
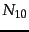 is the number of documents that contain
is the number of documents that contain 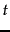 (
(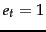 ) and
are not in
) and
are not in 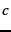 (
(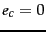 ).
).
 is the number of documents that
contain
is the number of documents that
contain 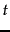 (
(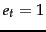 ) and we count documents independent
of class membership (
) and we count documents independent
of class membership (
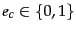 ).
).
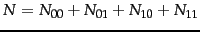 is the total number of documents. An example of one of the MLE
estimates that transform Equation 130 into Equation 131 is
is the total number of documents. An example of one of the MLE
estimates that transform Equation 130 into Equation 131 is
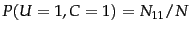 .
.
Worked example.
Consider the class poultry and the
term export in Reuters-RCV1. The counts of the
number of documents with the four possible combinations of
indicator values are as follows:
After plugging these values into Equation 131
we get:
End worked example.
To select 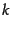 terms
terms
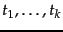 for a given class, we
use the feature selection algorithm in
Figure 13.6 : We compute the utility measure as
for a given class, we
use the feature selection algorithm in
Figure 13.6 : We compute the utility measure as
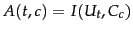 and select the
and select the 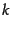 terms with the
largest values.
terms with the
largest values.
Mutual information measures how much information - in the
information-theoretic sense - a term contains about the
class. If a term's distribution is the same in the class as
it is in the collection as a whole, then
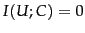 . MI
reaches its maximum value if the term is a perfect indicator
for class membership, that is, if the term is present in a document if
and only if the document is in the class.
. MI
reaches its maximum value if the term is a perfect indicator
for class membership, that is, if the term is present in a document if
and only if the document is in the class.
Figure 13.7:
Features with high
mutual information scores for six Reuters-RCV1 classes.
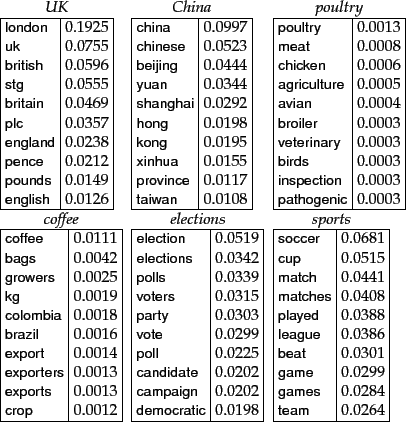 |
Figure 13.7 shows terms with high
mutual information scores for the six classes
in Figure 13.1 .![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png) The selected terms (e.g.,
london, uk, british for the class UK)
are of
obvious utility for making classification decisions for their respective classes.
At the bottom of the list for UK we find terms like peripherals and
tonight (not shown in the figure) that are clearly not helpful in deciding whether the
document is in the class. As you might expect, keeping the
informative terms and eliminating the non-informative ones
tends to reduce noise and improve the classifier's accuracy.
The selected terms (e.g.,
london, uk, british for the class UK)
are of
obvious utility for making classification decisions for their respective classes.
At the bottom of the list for UK we find terms like peripherals and
tonight (not shown in the figure) that are clearly not helpful in deciding whether the
document is in the class. As you might expect, keeping the
informative terms and eliminating the non-informative ones
tends to reduce noise and improve the classifier's accuracy.
Figure 13.8:
Effect of feature set size on accuracy for
multinomial and Bernoulli models.
![\includegraphics[totalheight=3in]{art/irnbayes7.eps}](img1042.png) |
Such an accuracy increase can be observed in
Figure 13.8 , which shows 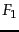 as a function of
vocabulary size after feature selection for
Reuters-RCV1.
as a function of
vocabulary size after feature selection for
Reuters-RCV1.![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png) Comparing
Comparing
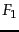 at 132,776 features (corresponding to selection of all
features) and at 10-100 features, we see that MI feature
selection increases
at 132,776 features (corresponding to selection of all
features) and at 10-100 features, we see that MI feature
selection increases 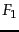 by about 0.1 for the multinomial
model and by more than 0.2 for the Bernoulli model. For the
Bernoulli model,
by about 0.1 for the multinomial
model and by more than 0.2 for the Bernoulli model. For the
Bernoulli model, 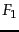 peaks early, at ten features selected.
At that point, the Bernoulli model is better than the
multinomial model. When basing a classification decision on
only a few features, it is more robust to consider binary
occurrence only. For the multinomial model (MI feature selection), the peak occurs
later, at 100 features, and its effectiveness recovers somewhat
at the end when we use all features. The reason is that the
multinomial takes the number of occurrences into account in
parameter estimation and classification and therefore better
exploits a larger number of features than the Bernoulli
model. Regardless of the differences between the two
methods, using a carefully selected subset of the features
results in better effectiveness than using all
features.
peaks early, at ten features selected.
At that point, the Bernoulli model is better than the
multinomial model. When basing a classification decision on
only a few features, it is more robust to consider binary
occurrence only. For the multinomial model (MI feature selection), the peak occurs
later, at 100 features, and its effectiveness recovers somewhat
at the end when we use all features. The reason is that the
multinomial takes the number of occurrences into account in
parameter estimation and classification and therefore better
exploits a larger number of features than the Bernoulli
model. Regardless of the differences between the two
methods, using a carefully selected subset of the features
results in better effectiveness than using all
features.





Next: Feature selectionChi2 Feature selection
Up: Feature selection
Previous: Feature selection
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() as
the expected mutual information (MI) of term
as
the expected mutual information (MI) of term ![]() and
class
and
class ![]() .
.![]() MI measures how much information the
presence/absence of a term contributes to making the correct
classification decision on
MI measures how much information the
presence/absence of a term contributes to making the correct
classification decision on ![]() . Formally:
. Formally:

![]() terms
terms
![]() for a given class, we
use the feature selection algorithm in
Figure 13.6 : We compute the utility measure as
for a given class, we
use the feature selection algorithm in
Figure 13.6 : We compute the utility measure as
![]() and select the
and select the ![]() terms with the
largest values.
terms with the
largest values.
![]() . MI
reaches its maximum value if the term is a perfect indicator
for class membership, that is, if the term is present in a document if
and only if the document is in the class.
. MI
reaches its maximum value if the term is a perfect indicator
for class membership, that is, if the term is present in a document if
and only if the document is in the class.
![]() The selected terms (e.g.,
london, uk, british for the class UK)
are of
obvious utility for making classification decisions for their respective classes.
At the bottom of the list for UK we find terms like peripherals and
tonight (not shown in the figure) that are clearly not helpful in deciding whether the
document is in the class. As you might expect, keeping the
informative terms and eliminating the non-informative ones
tends to reduce noise and improve the classifier's accuracy.
The selected terms (e.g.,
london, uk, british for the class UK)
are of
obvious utility for making classification decisions for their respective classes.
At the bottom of the list for UK we find terms like peripherals and
tonight (not shown in the figure) that are clearly not helpful in deciding whether the
document is in the class. As you might expect, keeping the
informative terms and eliminating the non-informative ones
tends to reduce noise and improve the classifier's accuracy.