Tf-idf weighting

We now combine the definitions of term frequency and inverse document frequency, to produce a composite weight for each term in each document. The tf-idf weighting scheme assigns to term 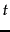$t$ a weight in document 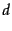$d$ given by

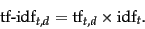$$\mbox{tf-idf}_{t,d} = \mbox{tf}_{t,d} \times \mbox{idf}_t.$$ (22)

In other words, 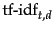$\mbox{tf-idf}_{t,d}$ assigns to term 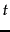$t$ a weight in document 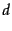$d$ that is

1. highest when 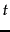$t$ occurs many times within a small number of documents (thus lending high discriminating power to those documents);

2. lower when the term occurs fewer times in a document, or occurs in many documents (thus offering a less pronounced relevance signal);

3. lowest when the term occurs in virtually all documents.

At this point, we may view each document as a vector with one component corresponding to each term in the dictionary, together with a weight for each component that is given by (22). For dictionary terms that do not occur in a document, this weight is zero. This vector form will prove to be crucial to scoring and ranking; we will develop these ideas in Section 6.3 . As a first step, we introduce the overlap score measure: the score of a document 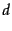$d$ is the sum, over all query terms, of the number of times each of the query terms occurs in 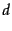$d$. 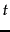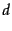We can refine this idea so that we add up not the number of occurrences of each query term $t$ in $d$, but instead the tf-idf weight of each term in $d$.

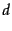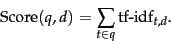$$\mbox{Score}(q,d)=\sum_{t\in q} \mbox{tf-idf}_{t,d}.$$ (23)

In Section 6.3 we will develop a more rigorous form of Equation 23.

Exercises.

• Why is the idf of a term always finite?

• What is the idf of a term that occurs in every document? Compare this with the use of stop word lists.

• Consider the table of term frequencies for 3 documents denoted Doc1, Doc2, Doc3 in Figure 6.9 .

  Figure 6.9: Table of tf values for Exercise 6.2.2.

  
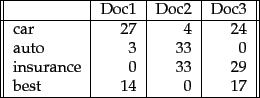  Compute the tf-idf weights for the terms car, auto, insurance, best, for each document, using the idf values from Figure 6.8 .

• Can the tf-idf weight of a term in a document exceed 1?

• How does the base of the logarithm in (21) affect the score calculation in (23)? How does the base of the logarithm affect the relative scores of two documents on a given query?

• If the logarithm in (21) is computed base 2, suggest a simple approximation to the idf of a term.