
N.B. This page is really old and out of date, and in fact I never really finished it in the first place...
Here I describe some of the topics I'm most interested in. To me, they all seem closely related, though I can't name the common thread. I do have some non-intellectual interests, but they hardly seem to deserve their own web page.
[This page is perpetually under construction, and consists mainly of gaps, punctuated by hogwash.]


Modular robotics is an approach to building reconfigurable robots for complex tasks. Instead of designing a new robot for each task, you build many copies of one simple module. By itself, one module can't do much, but when you connect many modules together you get a system that can do complicated things. A modular robot can reconfigure itself—change its shape by moving its modules around—to meet the demands of different tasks or different working environments. Shown above are the Digital Clay and Telecube designs.
The modular robotics team at Xerox PARC has produced some eye-popping MPEGs of their PolyBot climbing stairs, exhibiting snake and loop locomotion, and even riding a tricycle.
Marry modular robotics with nanotechnology and you get the shape-shifting "liquid metal" T1000 robot from Terminator 2. Yee haw.
In a sense, each of us is also a swarm of tiny modular robots: our cells. Unfortunately, we are not very reconfigurable. Our great-uncles the sponges (the most primitive of animals) have a very limited power of reconfiguration: if a sponge is forced through a sieve, its cells slowly reassemble themselves into a living animal.
Yes, we have a soul. But it's made of lots of tiny robots. —Giulio Giorelli
Nick Bostrom is an Oxford philosopher with lots of neat ideas. He asks questions like, Are You Living In a Computer Simulation?
Sometimes it seems as if the Universe has been designed just for us. Various physical and cosmological constants appear to have values fine-tuned to permit the development of intelligent life. What are we to make of this? Does it demand explanation?
One response is to interpret the appearance of fine-tuning as an observer selection effect. A selection effect occurs when a limitation of the data collection process introduces a bias in the results. For example, hundreds of thousands of sabre-tooth cat bones have been found in the La Brea tar pits, far more than anywhere else. Can we infer that most sabre-tooth cats met their deaths in tar pits? No, because our ability to gather data on sabre-tooth deaths is limited, and tar's ability to preserve biases the selection.
Some selection effects arise not from the limitations of some measuring device but from the inescapable fact that every observation requires the existence of a suitably positioned observer.
[...]
Barrow and Tipler offer multiple formulations of the Anthropic Principle:
Weak Anthropic Principle (WAP): the observed values of all physical and cosmological quantities are not equally probable but they take on values restricted by the requirement that there exist sites where carbon-based life can evolve and by the requirement that the Universe be old enough for it to have already done so.
Strong Anthropic Principle (SAP): the Universe must have those properties which allow life to develop within it at some stage in its history.
[...incomplete...]
Nick Bostrom maintains a good web site on the Anthropic Principle and observer selection effects.
Many famous mathematical conjectures (the Goldbach conjecture, the Collatz conjecture, etc.) have been verified by computer for millions or billions of specific cases, and are believed by most mathematicians to be true, yet continue to elude definitive proof. Other conjectures verified for many instances have since been falsified. Computers make possible a new way to study mathematical structures: through observation and exploration. Can induction from specific observations to general laws ever be justified in "empirical" investigations of mathematics? And what can the study of induction in a formal domain teach us about the use of induction in ordinary grubby reality? (This was the topic of my senior thesis at Princeton, for which I was awarded the Dickinson Prize for best senior thesis in logic and epistemology.)
Matter and mind, symbol and meaning, object and subject, action and intention, determinism and free will, substance and form, concrete and abstract, actual and imaginary, fact and interpretation. Here are some thoughts on philosophical dualities.
Suppose I have an infinitely large urn and an infinite collection of balls which are labeled 1, 2, 3, and so on. Consider the following experiment. At one minute before midnight, I put balls 1 through 10 into the urn, and then remove ball 10. (Suppose this takes no time.) At one-half minute before midnight, I put balls 11 through 20 into the urn, and then remove ball 20. At one-quarter minute before midnight, I put balls 21 through 30 into the urn, and then remove ball 30. And so on. How many balls will the urn contain at midnight?
Clearly, the urn will contain an infinite number of balls at midnight, since every ball whose number is not a multiple of 10 has been put into the urn and has not been removed before midnight. (Good thing it's a big urn.) However, now suppose that we modify the experiment slightly:
At one minute before midnight, I put balls 1 through 10 into the urn, and then remove ball 1. At one-half minute before midnight, I put balls 11 through 20 into the urn, and then remove ball 2. At one-quarter minute before midnight, I put balls 21 through 30 into the urn, and then remove ball 3. And so on. For this modified experiment, how many balls will the urn contain at midnight?
Surprisingly, the answer is now that the urn will be
empty at midnight. Any particular ball numbered
i will have been put into the urn, and later removed,
before midnight. (To be precise, ball i has been
removed at
This is already quite intriguing, but here's the kicker: now suppose that at each step, we randomly select one of the balls in the urn to remove. Now how many balls will the urn contain at midnight?
This example is due to Sheldon Ross, A First Course in Probability (sixth edition), p. 48.
Gabriel's horn is the surface of revolution generated by revolving the curve y = 1/x about the x-axis for x ≥ 1. Using integral calculus, we can determine that the horn has finite volume π, yet its surface area is infinite! Therefore no amount of paint is sufficient to cover the horn's surface, and yet the horn could be filled up using only π cubic units of paint. How can this be? (More details...)
Maybe everything that can happen, does happen.
In the standard Copenhagen interpretation of quantum mechanics, the wave function describing a system (such as a cat in a box) develops over time in either of two modes:
[Why has Copenhagen seemed necessary?]
Like many people, I find the Copenhagen interpretation pretty unsatisfying as a scientific explanation, because it raises more questions than it answers:
In 1957, a Princeton graduate student named Hugh Everett proposed a radically simple solution: there is no collapse of the wave function. The evolution of the wave function proceeds, always and everywhere, according to the (fully deterministic) Schrödinger equation. [explain consequences: superposition] This view has come to be known as the many worlds interpretation of quantum mechanics, although this appellation may be somewhat misleading, and many prefer to call it the many histories interpretation or (my own preference) the no-collapse interpretation.
[Why do people find MWI uncomfortable?]
[...incomplete...]
The work of Oxford physicist David Deutsch, and in particular his book The Fabric of Reality, which ties together four of my greatest interests: quantum physics, theory of evolution, theory of computation, and epistemology. Deutsch is more or less the father of quantum computing.
Max Tegmark is a hot-shit cosmologist at UPenn who seems to have written all the papers I wanted to (if only I were a hot-shit cosmologist). I like the fact that he's willing to write some papers he describes as "bananas", and he's interested in many of the same topics I am: the no-collapse interpretation, the anthropic principle, and the physics and metaphysics of information. To stretch your mind, try Tegmark's papers Does the universe in fact contain almost no information? and Is "the theory of everything" merely the ultimate ensemble theory?
The argument of Does the universe in fact contain almost no information? goes something like this. The universe appears to be staggeringly complex. To describe even a very small portion of it—such as a rabbit—would seem to require a vast and perhaps even infinite amount of information. However, this apparent complexity may be illusory, in the same sense that the Mandelbrot set, though apparently exceedingly complex, has a very small algorithmic information content: it is completely described by a comparatively short Turing machine program. Suppose the universal wave function shortly after the big bang had some quite simple form (say, a vacuum state) which could be described with very little algorithmic information. The Heisenberg uncertainty principle tells us that, at the microscopic scale, this initial state would involve superpositions of quantum fluctations in the gravitational field (and other fields). The time evolution of this state would involve non-linear elements which exhibit chaotic behavior. (As is well-understood, even the simple gravitational three-body problem exhibits a chaotic evolution.) Consequently, the micro-superpositions in the initial state are magnified into macro-superpositions. In the no-collapse interpretation of quantum mechanics, the current wave-function of the universe is thus a superposition of a vast number of states that are macroscopically very different. However, since macroscopic objects inevitably interact with their surroundings, decoherence prevents self-aware subsets of the universe (that's us!) from perceiving such macro-superpositions. So even though the univeral wavefunction contains very little algorithmic content, we experience a world that appears highly complex.
The possibly nutty Omega Point Theory of Tulane physicist Frank J. Tipler. Tipler argues that:

Many famous mathematical conjectures have been verified by computer for millions or billions of specific cases, and are believed by most mathematicians to be true, yet continue to elude definitive proof. What I find really interesting about such conjectures is the question of whether we should believe them on the basis of pseudo-empirical induction. Here are some prominent examples.
In 1742, Christian Goldbach wrote a letter to Euler in which he observed that, among all the even numbers he had examined, all greater than 2 could be expressed as the sum of two primes. For example:
|
4 6 8 10 12 14 etc. |
= = = = = = |
2 + 2 3 + 3 3 + 5 3 + 7 5 + 7 3 + 11 |
= = |
5 + 5 7 + 7 |
Since he observed a great number of instances of this rule, and no counter-instances, he advanced the conjecture known today as the 'Goldbach conjecture': "All even numbers greater than 2 may be expressed as the sum of two primes."
Mathematicians, who prefer theorems to conjectures, have tried again and again to find a proof of the Goldbach conjecture, but for over two centuries they have met only with failure. In modern times, computers have enabled researchers to verify the Goldbach conjecture for millions and billions of cases, and it is now known that there are no counterexamples to the Goldbach conjecture less than 20 million billion! But because we have no general proof that the conjecture is true, we must admit that a counterexample might be discovered.
This former conjecture gained widespread attention in 1994 when it was finally proven by Princeton mathematician Andrew Wiles. Previously, no general proof was available, although the conjecture had some truly remarkable inductive support. By 1993, it had been shown that in any counterexample to Fermat's Last Theorem, n is not less than 6,000,000, and a is not less than 101,800,000.
(A perfect number is equal to the sum of all its
positive divisors other than itself. For example, 6 is perfect,
since
A twin prime is one that differs from another prime by 2. For example, 11 and 13 are twin primes, as are 41 and 43. More than one hundred thousand twin primes are known.
| f(n) = { | 3n + 1 | if n is odd, | n/2 | if n is even. |
More informally: begin with any whole number. If it's even, divide by 2; if it's odd, multiply by 3 and add 1. Repeat until convergence. The Collatz conjecture asserts that no matter what number you start with, you will always arrive at 1. For example, if we start with 15, the sequence will be 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1.
The Collatz conjecture has been verified for all n less than three trillion.
Now that you know what it is, check out this xkcd cartoon about the Collatz conjecture.
Here's one I got from John McCarthy:
Two numbers m and n are chosen such that 2 ≤ m ≤ n ≤ 99. Mr. S is told their sum and Mr. P is told their product. The following dialogue ensues:
Mr. P: I don't know the numbers.
Mr. S: I knew you didn't know them. I don't know them either.
Mr. P: Now I know the numbers.
Mr. S: Now I know them too.
In view of the above dialogue, what are the numbers?
(To be strict, a number of additional assumptions are required: that both men know everything we do about the set-up, that both men are honest, that each man assumes that the other is honest, that both men are extraordinarily proficient at mathematical logic, that each man assumes that the other is extraordinarily proficient at mathematical logic, etc.)
I love this puzzle. What makes it interesting is the need for each man to reason about the other's reasoning. Also, the Goldbach conjecture turns out to be helpful!
John Conway's Game of Life has shaped my thinking more than almost anything I've ever learned about.
Despite his over-inflated ego and unwillingness to share credit, I admire Stephen Wolfram's big ideas.
The future of civilization is the future of technology. Everyone agrees on this, but opinions differ as to whether it's marvelous or terrifying.
Transhumanism is a sort of philosophy which takes a radically optimistic view of technology and the future. Transhumanists rejoice in using technology to expand human potential without limit, and take the view that the human species does not represent the end of our evolution but rather its beginning. Transhumanists are interested in all sorts of cool things like nanotechnology, superintelligence, virtual reality, uploading human minds into machines, posthumans, and the Omega Point Theory. Transhumanism is however sometimes tinged with looniness.
For a more somber view, I highly recommend reading Why the future doesn't need us, the much-discussed Wired article by Sun co-founder Bill Joy. He addresses the threat to humanity posed by the three defining technologies of the 21st century—artificial intelligence, genetic engineering, and nanotechnology—and the ethical issues faced by scientists working in those fields.
Questions about technology will become increasingly pressing over coming decades, as technological innovation makes ever greater worldly power ever more widely and cheaply available. We will soon come face to face with mega-terrorism, black-market military drones, custom virus kits, nanorobots in our bloodstreams, hybrid and synthetic life forms, and, before you know it, superintelligent machines who may find us a nuisance.
The defining global ideological conflicts of the 20th century were the struggle for control of the means of production and the confrontation between democracy and totalitarianism. What ideological and political battles will dominate the 21st century? There are many candidates: Islam vs. the West, globalizers vs. greens, rich nations vs. poor. I believe, however, that mastering the terrible power of technology will emerge over coming decades as the supremely urgent challenge facing humankind, and that the control of technology will become this century's defining political debate.
Trouble in nanoland is an excellent review of the current state of the nanotech industry from The Economist (12/5/02).
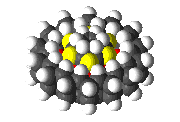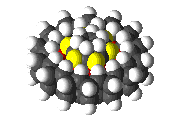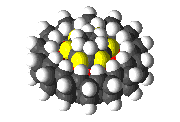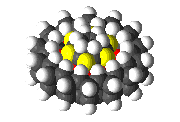
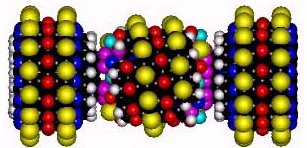
Designs for a molecular bearing and a molecular pump composed of 6,165 atoms.
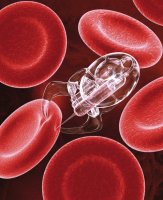

The vision of nanomedicine: a nanorobot delivers an injection to a red blood cell, while a bio-engineered cell rover swims through the body performing beneficial medical tasks. Um, assuming nothing goes wrong.
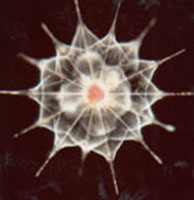
One of the more fantastic possibilities of nanotechnology is Hans Moravec's concept of the super-dextrous fractal robot, or bush robot. Inspired by biological models such as the basket star (below, right), a bush robot would resemble an animated bush, its largest part being a stem with swiveling branches, but its potency arising from trillions of swift nano-scale fingers. Armed with the right software and a big pile of dirt, a bush robot could build virtually anything in a few hours—including a replica of itself. It could also be a brilliant surgeon, or juggler.

Of course, designing the software to control a bush robot is a non-trivial problem. But current work on modular robotics may lead the way.
Here's the NASA study on bush robots conducted by Moravec in 1998-99.What are the limits to the plasticity of the human brain?
Consider color vision. We see colors well because we have trichromatic vision: our retinas contain three different kinds of photoreceptive cone cells, each sensitive to a different wavelength of light (red, green, and blue). In many colorblind people, one type of cone doesn't work. The resulting dichromatic vision yields a much poorer visual experience. However, many animals, including birds and fish, have four types of cones rather than three. The fourth cone is usually sensitive to ultraviolet light, giving these animals a broader range of visual experience than is available to us.
What if humans, like birds, had a fourth cone? To answer this question, Jay and Maureen Neitz at the Medical College of Wisconsin are working with a species of monkey that has only two kinds of cones. Using gene therapy, they hope to equip the monkeys with a third cone type. If their brains are able to process the new information, the monkeys might leap from dichromatic to trichromatic vision. Could similar techniques endow humans with tetrachromatic vision? And what would tetrachromatic vision be like? The vast difference between dichromatic and trichromatic vision gives us some hint. A fourth cone, says Jay Neitz, "would add two more entirely new colors, completely new and wonderful and unimaginable sensations. ...And it is not just those two new colors but the combinations of those colors with all the colors we already see. We would see almost everything differently."
It seems plausible, if speculative, that the brain could learn how to exploit this new hardware capability. But what are the limits? Could we develop pentachromatic vision? Could we add an entirely new sense, like the ability of hammerhead sharks to sense electrical fields? Could we learn to use a prehensile tail?
Anyway, here's more about the quest for super-vision.
Nature is still the most beautiful and ingenious designer.



Check out the Tree of Life web project: hypertext navigation of the Great Chain of Being, with tons of information, useful links, and many lovely photos.
It's hard to believe that a mollusk can be as smart as a mammal, until you watch an octopus hunting. Octopuses are the brainiest invertebrates by far: they can plan, learn, and remember what they learn. They master mazes faster than rats and pigeons. Some evidence suggests that octopuses are capable of observational learning, a hallmark of higher intelligence which many mammals lack. In a study published in Nature in 1992, an octopus learned to choose a red ball instead of a white one by watching another octopus. In another study, an octopus learned to open two bottles, one inside the other, in order to get at a fish inside. A few scientists even think octopuses use their wide repertoires of color displays as a form of visual language, with interchangeable component parts analogous to nouns and verbs. Needless to say, this view is controversial, particular since octopuses are not social animals.
It is the alien nature of octopus intelligence that fascinates me most. While the octopus's brain is as large as a mammal's, its neural architecture is completely different, which is not surprising given that the common ancestor of the vertebrates and the mollusks probably had no brain at all. The octopus nervous system is far more distributed than that of a vertebrate: as much as half of it is in the arms and suckers. And where a vertebrate has a single spinal cord, an octopus has dual nerve cords dotted with several pairs of ganglia—clumps of nerves capable of limited information processing. In the 1950s the U.S. Air Force funded research in octopus neurology, thinking it might help them to design better computers. But the octopus proved too complex for them.
Amazingly, octopuses evolved during the Cretaceous—long before whales and humans—and were probably the most intelligent creatures on Earth at that time. Since then they've been slacking. But if things had turned out differently, maybe they'd be running the planet now...
Read more on octopus intelligence and neurology in an excellent New Scientist article titled What is this octopus thinking?

Octopuses have many other remarkable traits. Their large, complex eyes endow them with excellent vision. They have three hearts, and their blood is blue because it uses a copper-based molecule to carry oxygen rather than iron-based hemoglobin. Their bodies are highly fluid: large octopuses can squeeze through astonishingly small apertures. Many octopuses can squirt ink, or change color almost instantly using pigment-bearing skin cells called chromatophores. The blue-ringed octopus of Indonesia (my personal favorite, shown above) can display pulsating waves of dazzling color—and it also has one of the most toxic venoms on Earth. The recently-discovered mimic octopus can, by modulating its coloration, its shape, and especially its behavior, convincingly imitate a lionfish, a predatory sole [QuickTime video], or a poisonous sea snake [QuickTime video]. It is the only animal known to mimic more than one other species.
There is some evidence that deep in the sea there lives a colossal octopus that can grow to over a hundred feet across and weigh 10 tons.
Octopuses belong to the phylum of mollusks and the class of cephalopods, a really cool group that also includes nautiluses and giant squids (ordinary squids too, I guess). And yes, it's "octopuses", not "octopi"—it's a Greek root, not a Latin one.
I'd like to be under the sea in an octopus's garden in the shade.

Jellies are not as smart as octopuses, but they have the same unreal beauty. Here are some QuickTime videos of jellies from the Monterey Bay Aquarium. Really trippy dude.






Polyclads are marine flatworms, beautiful animals with nasty relatives—they're closely related to the leeches in your swimming hole and the 60-foot tapeworms in your gut. Flatworms are among the most ancient of animal groups: biologists believe that flatworms were the first animals to develop bilateral symmetry, with a head, a rudimentary brain, and stereo senses. If this is true, then you and I are descended from creatures not too different from polyclads (and leeches, and tapeworms).
The polyclad has a bizarre sex life. Not only is it hermaphroditic, but each polyclad is equipped with two large penises. (Thus, on a per capita basis, the polyclad population has four times as many penises as the human population!) Polyclad sex is rough sex. Wielding their twin penises like swords, the polyclads engage in a violent bout of penis fencing, each struggling to the inject the other with its sperm. The loser is obliged to bear the burden of motherhood, and often suffers serious stab wounds as well. What would a feminist think?
Usually, polyclads glide over the sea floor, but occasionally they are seen propelling themselves through open water with undulating movements of stunning beauty. Unfortunately I can't find any movie files of this on the web, but here are some stills.


The polyclad is easily confused with another beautiful but entirely unrelated animal: the nudibranch, or sea slug, which is a mollusc.

Many nudibranchs contain chemicals which are toxic or distasteful to potential predators, and their bright coloration serves as a warning. It's not clear whether polyclads are equally distasteful, but many polyclads have evolved to mimic specific nudibranchs with remarkable fidelity, affording them a degree of borrowed protection.
Here's a great website on polyclads and nudibranchs.
Another fascinating topic: tiny Asian clams.