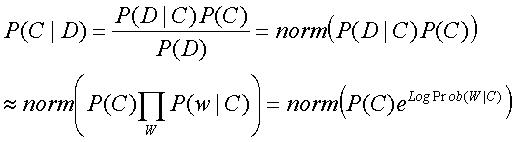CS 224N Final Project
Unsupervised Web Page Clustering
Spring 2000, Stanford Univ.
Paul Ruhlen – ruhlen@cs
Husrev Tolga Ilhan – ilhan@leland
Vladimir Livshits – livshits@cs
Introduction
Problem
With the huge proliferation of the World Wide Web, meaningfully
indexing or searching millions of non-homogenous documents has become an
increasing challenge and opportunity. We were curious how much structure
could be elicited directly from sets of web pages, with no supervised training
or "priming" of classifiers. While this unsupervised approach is unlikely
to achieve the accuracy of a hand-trained or constructed system, it could
suggest some lower bound on the need for expensive and slow human indexing
of the millions of new sites and pages being continuously added to the
Web.
Approach, Data, Evaluation
We decided to explore the behavior of the EM algorithm when
used for clustering a set of Web pages, in large part to gain experience
with issues of clustering and web processing. We initially decided to learn
a set of Naïve Bayes classifiers, one for each cluster, and to iterate
EM to Maximize the likelihood of the data given these classifiers, and
then use these new classifiers to re-assign the pages fractional membership
in the various clusters, according the their Expectation of being in each.
Our data were drawn from various categories or "topics"
in the www.dmoz.org directory. This directory is similar in purpose
and scope to Yahoo! and other web indices, although it is maintained by
a community of volunteer editors, and unlike Yahoo! dmoz.org
has an open licensing agreement that allows free use for derivative works,
such as this research. Selecting documents that were pre-categorized guaranteed
there was some underlying structure we could try to learn.
To evaluate our system’s performance, we carried along
with each page its original category string under dmoz.org, such
as "Sports/Badminton/". To measure the quality
of the current learned clusters, we found, for each cluster, the most frequent original category
string among its members (counting as members only items with a higher
fractional expectation of being in this category than in any other). Then
every member that matched this most frequent original category was counted
as correctly categorized, and any other member was counted as an error.
This measure of accuracy had the advantage that achieving 100% percent meant
we had exactly re-created the original clusters. It had the disadvantage
that no "partial credit" was given for clustering similar documents together
that happened to have been originally indexed separately, perhaps arbitrarily or mistakenly
by a human editor. (We discovered at least once such mis-categorization,
when a site on Chinese calligraphy ended up counting as an error in our
calligraphy cluster, because it had been indexed under sculpture.)
It also gave no direct penalty to splitting an original
single cluster into two or more parts, although such a split guaranteed
that members of at least one other cluster would have to be counted as
errors, since there would not be enough remaining clusters to go around.
Findings
We achieved surprisingly good accuracy rates on sets of up
to 300 pages, drawn from up to 8 categories, reaching average accuracies
across multiple runs as high as 92%. The approach did not seem likely to
scale well up to thousands of categories without substantial redesign.
Literature
We actually did very minimal literature review when starting
this project, in part because of the very limited time for the project,
and because we felt we would learn a great deal just "getting our hands
dirty" with attempts to build and improve a clustering system.
We did take a close look at Hierarchically classifying
documents using very few words, by Koller, D., Sahami, M., Proc. of
the 14th International Conference on Machine Learning ICML97, pp. 170---178,
1997.
While this was a semi-supervised learning system, classifying
computer science research papers into an existing hierarchical category
tree, it did train Naïve Bayes classifiers using EM to let a large
body of unlabeled training data improve the performance of the classifiers.
It also used an extension to NB classifiers that learned limited dependencies
among words, and learned a hierarchical set of classifiers, to reduce the
size and scope of each classifier and improve reliability.
We also took a quick look at: A Corpus-Based Investigation
of Definite Description Use, Massimo Poesio, Renata Vieira, Centre
for Cognitive Science, The University of Edinburgh,
and a few other papers on Kappa as an alternate measure
of the reliability of our clusters. We decided that consistency of
learned clusters from one run to the next was less meaningful than agreement
with human editors, since learning such inane clusters as alphabetic
ranges of the first word of the document would be completely consistent
and repeatable, but equally useless as category clusters.
Design and Algorithms
The system we designed has two major parts:
a Perl script for downloading, parsing, filtering, and caching the URLs
as files of tokens, and a C++ program for reading and clustering the
resulting files, and measuring the accuracy of the learned clusters.
Download and HTML Parse
We decided early on to download and cache web pages, in order
to isolate our clustering tests from the often slow response times of some
web servers, and to improve repeatability in testing, since pages that
were present in one download might be unavailable the next. We chose Perl
to implement this portion of the system, due to its strong features for
network and socket I/O, ease of text processing and filtering, and extensive
library modules. Most HTML tags were completely removed from the text, leaving
only the visible plain text from the web page, with no formatting information
remaining.
We also chose to implement an optional stop-word list
at this point, to remove high-frequency low-information common words. We
started with a list of generally common English words, and supplemented
it during development with vocabulary common to web pages, such as click,
e-mail, visit, and site, with our final set including 156 words.
Stop-word filtering, like most features of the script, could be controlled
through command-line options, so comparative tests were simple to perform.
We also stripped out all characters other than letters,
hyphens, apostrophes, and periods, and then dropped all tokens that contained
no letters, or that were shorter than four characters. For almost all testing
we shifted all text to lower-case, to better smooth the text distribution.
We eventually decided to parse the META tags for Keywords
and
Description, and include their text along with the page title in the cached
file, each surrounded by delimiter tags so the cluster program could choose
whether to include or even emphasize those words. This particularly helped
classify some minimal pages that were the top of an HTML frame set or contained
only a "splash" image. In keeping with the ever-changing structure of the
Web, we discovered a fairly high fraction of pages listed in the
dmoz.org
directory
were just "Click here for new location" pointers, or were frame sets or
splash pages with no META tags or other significant text. A more sophisticated
front end could try to recognize such pages and download the new location
or child pages. We decided to simply discard pages that were shorter than
150 characters, once keywords, title, and description were included, which
removed most of these unclassifiable pages from our test sets.
In our largest test set of 1493 URLs, 97% of the pages
downloaded without an error, and of those, 75% passed the length threshold
and were cached for clustering.
The initial version of our Perl front end would simply
take a file of URLs and dmoz.org category strings, download, parse,
and filter each one, and store it in a text file named after the original
URL. It would also create an index file, containing all the filenames and
category strings, which would serve as the initial input to the clustering
stage. As we expanded our testing to cover larger and more challenging
test sets, it became cumbersome to hand-construct the URL files. So we
expanded the capabilities of our front end to be able to take a set of
dmoz.org
categories and create a URL file by reading the dmoz.org directory
contents directly. Finally, in order to be able to create arbitrarily large
test sets for scalability testing, we added the ability to randomly walk
the dmoz.org directory and generate any number of "leaf node" categories.
Initialization
Our C++ clustering program scanned the index
file generated by the front end, and for each file listed, created a new
Document object, appended onto a list of Documents. It opened the file and read
in all the tokens in the file into a word frequency "map" member of the
Document, and filled in the original dmoz.org category string as
another member. This original category was completely ignored by all clustering
algorithms, and used only by the evaluation routine for judging the accuracy
of learned clusters. The word frequencies were then normalized within each
Document to sum to one, so that they represented the probability of a random
token in that Document being of that type. Since each document’s
word frequency map contained only the filtered words in that particular
document, it was much smaller than a smoothed distribution across the entire
vocabulary, and could be processed more quickly.
We implemented various attempts at elimination "noise"
words that were beyond what a fixed stop-word list could accomplish. An
option (-r) would prune the word frequencies to remove all words that occurred
in only one Document, since we considered learning single-document clusters
to be outside our domain, and we learned that "outlier" pages could otherwise
dominate some classifiers. Such words could obviously contribute no positive
evidence in learning which documents to cluster together.
We also experimented with an option (-m N) to further
prune the word frequencies to preserve only the N words in each document
that occurred across the largest number of different documents. Any word
in the entire vocabulary flagged to be thus preserved by any document was
preserved in all documents, and all other words were deleted in every document.
Other options would delete words in each document that
occurred £ N times (-f N), so –f 1 discarded
singleton words, or would keep only the N most frequent types in each document
(-k N). After all such pruning of word frequencies, they were renormalized.
K-means
We experimented briefly with a K-means clustering algorithm,
as had been suggested in the review of our project proposal. In this algorithm,
documents are randomly assigned to some single cluster, then each cluster
constructs a "centroid" word frequency distribution averaged across all
its member documents. Then documents are iteratively re-assigned to the
cluster with the closest centroid, using as a distance measure the dot
product between the centroid and its word frequency, both being re-normalized
as a unit vector. Iteration halts when documents stop moving between clusters.
We implemented K-means as "hard" clustering, in which
each document belongs to only the closest cluster.
EM Algorithm
We spent considerably more time experimenting with a version
of the Expectation-Maximization algorithm, which uses "soft" clustering
of fractionally assigning documents to multiple clusters, based on their
probability of belonging to each cluster (the Expectation phase). Then
it constructs each cluster’s classifier based the average across its member
documents, each weighted by their fractional expectation of being in that
cluster (the Maximization phase).
The halting condition is based on each document comparing
its old vector of Expectations to the new one after each E-phase, finding
the largest absolute change in the vector, and then finding the largest
of these changes across all documents. If this maximum Expectation change
is below some threshold (0.0001 for most of our testing), we conclude
that EM has converged and halt.
We implemented two types of classifiers for use with the
EM algorithm, with a command line option to select which one to use.
Naïve Bayes Classifier
For the Naïve Bayes classifier, each cluster maximized
the likelihood of the documents that fractionally belonged to it by constructing
an average word frequency distribution across them, much like the K-means
centroid, but weighted by the expectations. Smoothing of this distribution
(to avoid any 0 probability words) was achieved by smoothing all the expectation
vectors slightly. By ensuring that every document had at least a non-zero
epsilon
membership in each cluster (set to 10-10), this guaranteed that
each cluster gave every word across the full vocabulary of the test set
a positive probability.
For each document’s expectations, it passed its word frequency
map into the LogProb method of each cluster, and got back the Log Probability
of that document "occurring," conditional on it being from that cluster. LogProb
calculated the sum across every word in the document’s word frequency of
the log of the product of that frequency and the classifier’s probability
for that word. In probability space, this is the equivalent of computing
the product across each word w in the document of P( w|
c), which the Naïve Bayes assumption substitutes for the probability
of the full document given the cluster, by assuming the individual words
occur independently. This math is all done in Log space to avoid the risk
of underflow from multiplying together many very small probabilities.
We calculate for each document D, for every cluster
C:
where "norm" simply renormalizes each term as a probability
by dividing by the sum of all terms across clusters. We chose to ignore the prior probability
of each cluster P(C), assuming that every cluster was equally probable
(i.e., of equal size). To calculate the exponent term, since the normalization
needs to be done in Probability space, not Log space, we first subtracted
from every LogProb the largest (most positive) LogProb value, then took
the exponent of each term and normalized them. This subtraction was equivalent
to multiplying each probability by the same (very large) constant value,
which avoided underflow that would result from taking the exponent of such
large negative numbers, and then disappeared when normalized.
Cosine Similarity Classifier
We also implemented a classifier based on the cosine similarity
measure, instead of the NB probability, which in effect assumed that P(D|C)
was proportional to vector cosine between the document’s word frequencies
and the cluster’s centroid. This was not really mathematically justified,
since unless these two vectors were almost completely orthogonal, meaning
they shared no word in common with more than a tiny frequency, they would
have some significant similarity.
This approach was really a "soft" variant of K-means clustering,
permitting (and almost guaranteeing) fractional membership in multiple
clusters, but using Euclidean distance for expectation weightings rather
than a strictly probabilistic formula.
Results
Nonetheless, using EM with the cosine classifier gave
us our only successful clustering behavior, and formed the basis for most
of our further experiments and extensions.
K-means clustering never iterated more than once, because
no document ever moved from the cluster to which it was initially (and
randomly) assigned. Apparently, such "hard" clustering on the relatively
small sets of data points (hundreds of documents), and the high dimensionality
of the parameter space (
10,000 words in the vocabulary), meant that any
set of documents could find a centroid along some "word dimensions" that
was closer than those any other sets.
Perhaps more surprisingly, the Naïve Bayes classifiers
behaved quite similarly, in that documents rarely switched from the clusters
to which they were first randomly assigned. We used various diagnostics
to examine the causes, and discovered that almost every document contained
words that were infrequent in other documents and therefore in other clusters.
Since the membership of the document in its initial cluster guaranteed
that every word in the document had a value in the classifier significantly
greater than zero, it’s probability P(D|C) was significantly greater than
zero in its cluster. But since every other cluster almost always had tiny
epsilon
smoothing values for one or more words in the document, the product of
the probabilities across all words was nearly zero, even if many other
words were a good match in frequency.
So the negative evidence of even one "missing" word in
another cluster was enough to lock documents out of almost ever preferring
a new cluster and switching.
We tried several variations in an attempt to "shake loose"
this rigid stability of the NB clusters. We aggressively smoothed the expectation
vectors (option –s), and thus the classifier distributions, by adding 1.0
to each expectation in the document and renormalizing. This was equivalent
to setting each expectation E to (E+1)/(N+1), where N is the number of
clusters, or an interpolation of each E with 1/N. The result was that expectations
started and remained more evenly spread across the clusters, but a cluster
that started with a slight lead over the others for a document, tended
strongly to maintain that lead. Expectations tended to converge quickly
to 2/(N+1) for the initial cluster and 1/(N+1) for the others. This was
again due to the power with NB classifiers of negative evidence, even though
this was somewhat weakened by every cluster having a significant fraction
of each document’s word frequencies.
Another variation was in initialization of expectations
before the first M-phase (-i option). Rather than assign each document
entirely to a single cluster (except for the epsilon smoothing),
each expectation was set to 1/N, and then slightly randomly perturbed by
up to 1%. This too had little effect on the pattern of rigid convergence
to the initially leading clusters, even when combined with the aggressive
smoothing option.
Fortunately, the behavior of the "soft" cosine was much
more promising. On our simplest test set of 22 documents from only 2 categories,
the base cosine measure, with no additional options, achieved 100% accuracy
on 20 out of 20 runs with different random starts. The random initial assignments
had accuracies of between 54% and 72%. Throughout our tests with cosine,
it always significantly improved accuracies over the random starting positions.
While accuracies on the more complex test sets did vary with starting position,
the best results were never due to the data already being "pre-clustered"
by the random start.
When we ran the system on our next most difficult test
set, "Set2" consisting of 73 URLs drawn from 5 widely-spaced different
dmoz.org
categories, we began seeing more complex patterns of convergence. In particular,
the accuracy would always peak in accuracy and decline, usually within
5 iterations, at an average of 84% correct, but then continue iterating
another 60+ times before the Expectation deltas converged, with a final
accuracy averaging below 69%.
Clearly what EM was minimizing in its gradient descent,
the differences between the cluster centroids and the fractional document
expectations, did not map precisely to minimizing deviation from the original
human-generated category labels. These two were clearly related, however,
in that EM consistently reached a much-improved level of accuracy before
overshooting on its way down its error slope.
At this point we implemented and tested several of the
options described above, including pruning out words on various criteria,
and options to emphasize words in the title (-e N) or in META tag keywords
(-y N), counting such words as though they occurred N times instead of
just once.
We discovered that the cruder methods for removing infrequent
"noise" words substantially reduced accuracy. When we examined some basic
word counts across the cached text files, we discovered that infrequent
words often contained critical information about the topic of the page.
For example within a Badminton category, of the 12 documents that contained
the word "badminton," 4 of them used it only once, so stripping out singletons
within documents, or keeping only the N most frequent words, discarded
important information more than it filtered out irrelevant noise.
Since peak accuracy seemed to vary widely from run to
run, even with the same options, we realized we needed to perform multiple
runs to reduce the stochastic noise in our accuracy measurements. We used
a set of simple scripts to let us run batches of 20 runs with a particular
set of options, store the results, and filter out the significant numbers.
Among the options that did not severely reduce peak accuracy (see Figure
1), there was disappointingly little variance from the base (no options)
system. Since there is still some stochastic noise from random starting
conditions in this data, even averaged over 20 runs, differences of 1 or
2% in accuracy could easily be due to chance, rather than a true difference
in performance. Emphasizing title words slightly hurt performance, probably
due to the many non-descriptive titles such as "Anne’s Corner of the Web."
Emphasizing keywords by 5 seemed to help a bit, although tests on other
sets would should such emphasis having a negative effect.
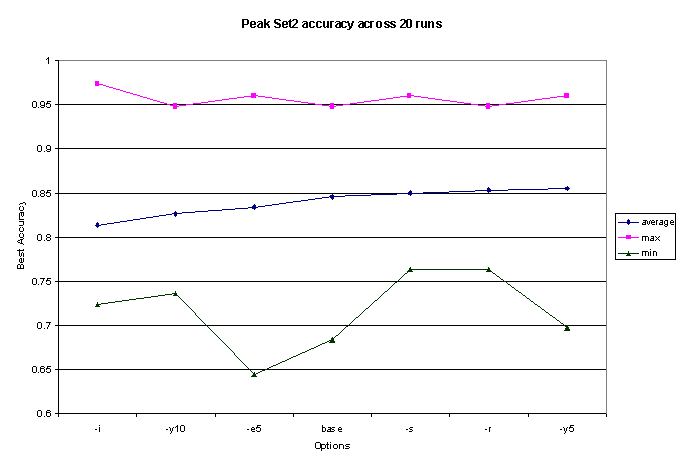
Figure 1
We also experimented briefly with trying to "guess" where
the peak accuracy would occur, so we could halt EM iterations at that point.
We noticed that, even across test sets, there was a consistent "elbow"
in the curve of declining expectation deltas around the point of maximum
accuracy. So we constructed a measure of the second derivative of Expectations
that could usually predict within one or two iterations where a good halting
point would be.
We also noticed a pattern that one or two clusters tended
to go "extinct" in most runs. While they still could contain some fractional
expectation of some documents, no document had them as their highest-expectation
cluster when EM converged, and so they contributed nothing to the final
accuracy score.
Clearly though, a different approach was needed to significantly
improve system performance, and to more robustly deal with the disconnect
between peak accuracy and convergence.
Enhancements
Information Theory and Feature Selection
In discussions with Dan Klein, he suggested we concentrate
on some form of "top-down" identification of the relatively few words that
are the best features for distinguishing the clusters, rather that
a "bottom-up" attempt to eliminate the worst words. This brought to mind
the use of information theory in decision tree learning for selecting a
feature to "split" the tree on at any point, by calculating the information
gain after each possible split (or equivalently, the reduction in entropy).
To accomplish this, we added an entropy option (-h K)
that would keep in each classifier, in each M-phase iteration, only the
K words with the lowest entropy for distinguishing documents being inside
the cluster vs. outside. Besides calculating the normalized classifier
as the expectation-weighted average of member documents’ word frequencies,
we also constructed an "anti-classifier" for each cluster, of the average
weighted distribution of words across all the other clusters. We
could then examine each pair of frequencies of each word, and calculate
the entropy using the following formula. We developed this ourselves, having
not found an equation for information gain based on fractional data samples,
with the counts of data instances (documents) all normalized away.
For each word type w, let fw be the frequency
with which it occurs in the current cluster, and fw’ be its
frequency across all other clusters. Then the probability of being in this
cluster given that the word occurs is Pcw+ = fw / (fw
+ fw’ ) and the probability of being in a different cluster
given the word occurs in 1 – Pcw+. The probability of being in this cluster
given the word doesn’t occur is Pcw– = (1 – fw ) / ((1 – fw
) + (1 – fw’ )) of being in a different cluster, 1 – Pcw–. Also
the overall probability of the word occurring, assuming N equal–sized clusters,
is the weighted sum of fw and fw’,
Pw = (fw / N) + fw’ ´
(N – 1) / N. Then the entropy of cluster membership given the word occurred
is
Hw = – (Pcw+ ´ log Pcw+)
– ((1 – Pcw+) ´ log (1 – Pcw+)) bits.
And the corresponding entropy given the word not occurring is Hw’ = – (Pcw–
´
log Pcw–) – ((1 – Pcw–) ´ log (1 – Pcw–))
bits. And the total expected entropy from knowing whether this word occurred
is the weighted sum of these two values:
Htotal = Hw ´ Pw + Hw’
´
(1 – Pw).
Testing with a pair of artificial documents with only
a handful of words confirmed that Htotal has the desired behavior that
it is 1 (no information gain) for words with equal distribution in and
out of the cluster, and it’s lowest for words that occur only in one distribution
but not the other. And for different word pairs with the same ratio of
frequency, it’s lower for words with higher overall frequency (so the pair
0.04, 0.02 scores lower than the pair 0.02, 0.01).
The system builds a list of all the words in the classifier
and their Htotal values, sorts it in ascending order, and removes all but
the K lowest scoring words from the classifier. Although Htotal is symmetric
whether the evidence of the word is positive or negative for membership
in the cluster, (fw > fw’ or vice versa), our experience
with Naïve Bayes classifiers led us to believe that the absence of
a word was rarely a useful indicator. Only word pairs with fw
> fw’ were considered when selecting the K best features.
The improvements when testing on our larger more complex
data sets were impressive. On Set3, containing 201 documents drawn from
7 more closely-related categories (3 under the visual arts, 2 under radio),
the average peak accuracy jumped by 5% or more over any of the other enhancements
we had attempted (See Figure 2). Just as importantly, using almost any
value for –h K nearly eliminated problem with large declines in accuracy
before convergence, and clusters going extinct. EM always converged at
or within one or two documents of the highest accuracy achieved by any
run using this feature selection (See Figure 3). And the rate of clusters
going "extinct" fell dramatically as well, from 77% of runs on Set3 converging
with 4 or more empty clusters (out of 7) to less than 6% of runs converging
with a single empty cluster.
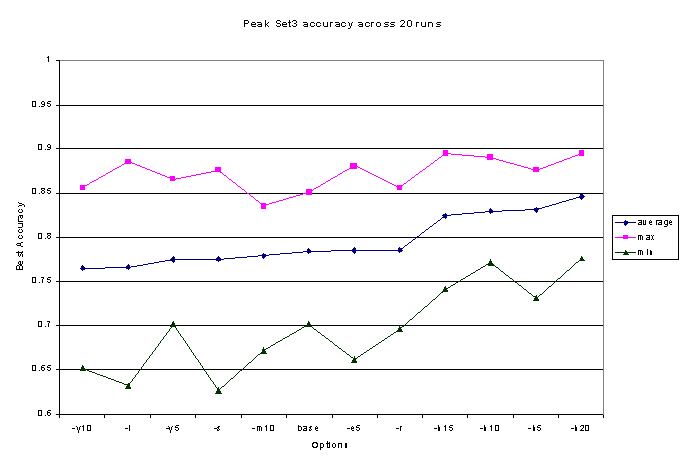
Figure 2
Also interestingly, our diagnostics displayed the words
selected for each classifier after the final iteration (or in verbose mode,
at every iteration), and these words often read like human-selected keywords
for identifying that category. For instance, a Set3 "Radio Guides" cluster
learned "radio, stations, live, world, music, audio, online, broadcasting,
country, station, television, rock, and broadcast" as its highest-information
words, and another on Calligraphy learned "calligraphy, lettering, hand,
design, invitations, wedding, calligraphers, calligraphic, guild, calligrapher,
join, gift, and weddings"
Both numerically and subjectively, this method of identifying
relevant vs. irrelevant words was far superior to our other attempts.
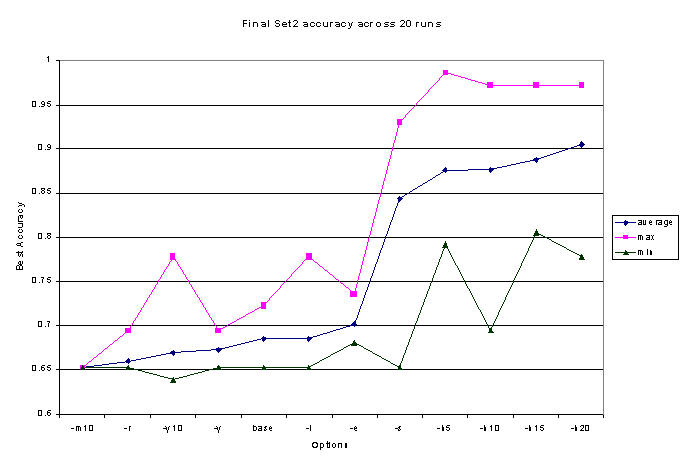
Figure 3
It did still have limitations, and our average accuracies
across runs remained bounded at about 92% in Set2 and 87% for Set3 (see
Figures 4). For Set2 the best accuracy was achieved with a relatively small
set of K features, 10 or 20 words, while for Set3, accuracy continue to
slightly increase up through 70 words, the largest we tested. This is probably
due to the fact that the categories in Set2 are widely spaced, so few words
are needed to distinguish between them, and a smaller set of higher-frequency
words is less noisy and smoother. But with Set3’s closely-related categories,
a much larger set of words is needed to simultaneously distinguish each
cluster from both distant clusters and its nearby "siblings."
In examining the final clusters learned we also noted
a problem when trying to learn clusters of very different sizes. The larger
categories would often split their documents between 2 clusters, one of
which would subsume a much smaller category, by including a few key words
that identified those documents better than any other cluster. But most
feature words were identical to the classifier for cluster with the other
half of the documents from this category. The fractional expectations of many
of these large-category documents was split almost evenly between these
two clusters, while the subsumed smaller category documents generally had
expectations close to 1 of being in their cluster together. Even when small
clusters were successfully learned, it was clear from the fractional expectations
of documents in large clusters, and the high-information feature words
of the smaller clusters, that they had a large number of documents from
the larger cluster with significant fractional membership in the small
cluster. So even then a larger cluster was close to dividing and subsuming
the small cluster.
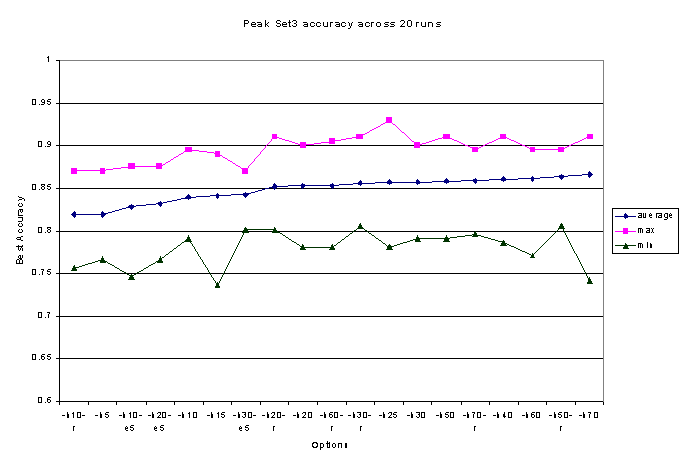
Figure 4
We ran out of time to really analyze and address this
limitation. One possible approach would be to somehow discount "minority"
fractional members of a cluster in favor of members with a very high expectation
of membership, in particular when the number of fractional members is very
large compared to the high expectation members. Another would be to examine
our assumptions our expected entropy calculations about equal-sized clusters,
and consider removing or weakening any current bias towards learning clusters
of roughly equal size.
Scalability
We wanted to know whether our algorithms would still perform
well when scaled up to much larger sets of clusters and documents. Unfortunately,
our first attempt at feeding in a test set with almost 1500 hundred pages
and 96 clusters quickly revealed we had implemented several routines in
a highly non-efficient manner, and completing even a single run to convergence
would take days. Some simple optimization changes let us run the base version
of our EM with cosine classifiers for one run, taking several hours to
do so, and accuracy peaked at 51% on the second iteration and then declined
to %15 (about the same as the initial accuracy) over 20 iterations, converging
with 81 of the 96 learned clusters being empty. The complexity of our algorithm
when learning N clusters over D documents, each with an average internal
vocabulary size of V was O(NDV), so while V remains fairly fixed, run time
blows up fairly quickly when both N and D increase by an order of magnitude.
Unfortunately, our algorithm for computing information
gain for feature selection would need considerable redesign to be able
to run faster than O(N2DV), so each iteration would take upwards
of 8 hours on this largest set. We scaled back the set size to 48 clusters
and 454 documents, and a single run using the –h 50 option reached an accuracy
of 68% in 13 iterations then slowly declined to 65% over another 90 iterations,
when we terminated it after 14 hours. Clearly substantial redesign and
testing would be needed before this approach could successfully cluster
any large portion of the full dmoz.org directory, if then.
Final Test
We also reserved a final test set that we had not used in
development, similar in size to Set3, and ran a final sequence of test
runs against it using "-r –h 50" options, which had performed very well
on Set3. 40 test runs produced an average accuracy of 78%, max and min
of 84% and 70%, respectively, which were lower than on Set3, but by less
than 5%. This reasonably high performance seems to indicate we had not
overfit our stop-word list, algorithms, or other options to our development
test sets.
Conclusions
We achieved a fairly high level of agreement with human
editors in clustering moderately-sized sets of web pages, even when topics
were closely related. Examining some of the mis-classified pages on our
better test runs showed that many of them were probably unclassifiable
based on only their content text, being longer-than usual "we’ve moved"
pages, "choose hi/lo BW" or other splash pages. And a few were extreme outliers
in word frequency for their category, such as a Palm Pilot page that never
used words like palm, pilot, handheld, or software.
The improvements from information gain feature selection
were impressive, particularly considering our fairly casual understanding
of the theory behind it. A more complex application of information theory
might be the best way to address the remaining problems of large clusters
consuming smaller ones, clusters going empty.
The scalability of this approach remains a major weakness,
and it might never scale to domains of hundreds of categories or more, even
with further analysis and optimization. But it does seem to indicate that
a simple text frequency analysis contains extremely relevant information
about the topical similarity of pages. Such clustering might be a reasonable
first stage when creating an index of smaller sets of documents, such as
the pages within a company or departmental web site.