Matthew
Chiu
CS224N
June
5th, 2001
Final Project
Introduction.
The goal of my final project is to build a text summarization system, a system that selects whole sentences from a document to form a summary. I chose to base my project on the system described in “A Trainable Document Summarizer” (Kupeic, Perdersen and Chen 95 [1]). Kupeic et al. presented a method of training a Bayesian classifer to select sentences from documents according to several heuristic features. Their work focused on analyzing single documents at a time.
Since then, there has a been lot of work on the
related problem of Multiple-document Summarization (Barzilay et. Al 99 [2],
Radev et. Al 98 [3]), where a system summarizes multiple documents on the same
topic. For example, a system might summarize multiple news accounts, of the
recent massacre in Nepal , into a single document. I was also interested in
comparing documents, not to combine multiple documents into one, but to improve
upon the summary of a single document.
My hypothesis is that the similarities and
differences between documents of the same type (e.g. bios of CS professors,
earnings releases, etc.) provide information about the features that make a
summary informative. The intuition is that the ‘information content’ of a
document can be measured by the relationship between the document and a corpus
of related documents. To be an informative summarize, an abstract has to
capture as much of the ‘information content’ as possible.
To gain a handle on the problem of capturing the
relationship between a document and a corpus, I examined several papers on
Multiple-Document Summarization. However, I found most of their approaches were
not applicable to my problem since they are mostly trying to match sentences of
same meaning to align multiple documents. My system has to find the common
topics in a corpus by matching sentences that are saying different things about
the same topic (e.g. next quarter’s earning’s forecast in earnings releases).
Favoring simple techniques, I decided to represent
the body of documents as a vector space. This approach has been used in many
successful applications such as the SMART Retrieval System (Salton 71 [4]). I
defined my problem as finding the common topics in a corpus (each topic also
being represented by a vector). There are many algorithms that try to
‘discover’ the hidden dimensions in data; a well known and simple approach
being Principal Component Analysis. My project is strongly motivated by the
analogy between this problem and the problem of face identification, where a
system learns features for facial identification by applying PCA to find the
characteristic eigenfaces.
Training a
document summarizer
My
document summarizer is based upon (Kupeic 95) except I modified it to add a new
feature based upon the results of comparing the document to its corpus.
Kupeic
et. Al describe a method of training a Bayesian classifier to recognize
sentences that should belong in a summary. The classifier estimates the probability
that a sentence belongs in a summary given a vector of features that are
computed over the sentence. It identifies a set of features that correspond to
the absence / presence of certain words or phrases and avoids the problem of
having to analyze sentence structure. The following are the features that they
trained their classifier on:
Sentence Length Cut-Off Feature:
a binary feature with a value of 1 if the sentence is longer than 5 word.
Fixed-Phrase Feature: The
feature value is 1 if the sentence contains any of 26 indicator phrases such as
“in conclusion”.
Paragraph Feature: Sentences
are classified as paragraph-initial, paragraph-medial, and paragraph-final.
Thematic Word Feature: Words
that occur often are considered to be thematic words. Each sentence is scored
according to how many thematic words occur. Then some fraction of the
top-scoring sentences are given a feature value of 1, and the others a value of
0.
Upper Case Feature: Similar
to the thematic word feature, except the words being considered are upper case
words, which should correspond to proper nouns.
All
of the features are binary except for the Paragraph feature which can take on
one of 3 values. The probability that a sentence belongs to the summary given
the feature vector can be reformulated in terms of probability of a feature
vector given the sentence by Bayes rule:
![]()
If
we assume that the features are statistically independent then we can estimate
the probability of each feature independently, and multiply them together to
arrive at the probability of a feature vector given the sentence.
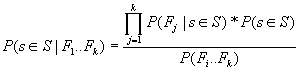
![]()
At
this point, I simplified their approach by noticing that the size of the
feature vector has 3*2*2*2*2 or 24 possible values. Therefore, the Joint
Probability Distribution of s,F has 48 possible values. It is possible to
directly estimate the Conditional Probability Distribution from the data
without making any independence assumptions.
![]()
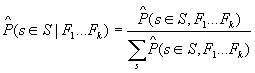
After
testing each feature individually, Kupeic et Al. found the best performing
feature to be the Pargraph feature. On the other hand, Thematic Word feature
and the Uppercase Word feature performed the worst. One reason why the Thematic
Word feature didn’t perform as well as expected was because words that occur
often are not necessarily best indicators of the topic.
For this project, I decided to create a new feature
called the ‘topic feature’ which has a value of 1 if the sentence is relevant
to the topic and 0 otherwise. Following their approach, the system scores
sentences according to how many topic key-words it contains. The top scoring
sentences are given a feature value of 1 and the others zero. Thus, it is
similar to the upper-case feature and thematic-word feature with a different
set of words. For the purposes of comparison, I also implemented the Paragraph
feature, the Uppercase Feature, and the Thematic Word Feature.
Applying Principle
Component Analysis to document vectors
To
create my topic feature, I needed to find words which are indicative of the
topics that are common to the corpus. As I discussed in the introduction, the
approach is to apply Principal Component Analysis to documents represented as a
vector space.
1.
Using Singular Value Decomposition (SVD) to find the principal components of a
vector space.
- The vector
representations of the documents, collectively define a n-dimensional
vector space (where each document is a nx1 vector).
- The m document vectors
taken as the columns of a nxm matrix D, define a linear transformation
into the vector space.
- Every matrix can be
written as the product of 3 matricies
![]()
where U, V are orthogonal and S is diagonal (corresponding to a rotation to
a new representation, stretching and rotating back). The columns of V are the
‘hidden’ dimensions that we are looking for. The diagonal of S are the singular values which are the
weights for the new set of basis vectors.
- Computing the svd of
the matrix can be accomplished by a computationally simpler process. We
compute the mxm outer product (where matrix element i,j is the inner
product of documents i and documents j). This mxm matrix is symmetric, its
singular values are its eigenvalues and its basis vectors are the
eigenvectors. Given a eigenvector e, we can find the corresponding
dimension in document space.
![]()
2.
Modeling the corpus as a vector space
The simplest way to transform a document into a
vector is to define each unique word as a feature. The weight of a feature
being the number of times it occurs in that document, commonly referred to as
the ‘term frequency’. The biggest problem with this approach is that words such
as ‘the’ are far more common than others yet provide very little information
content.
A common fix for this problem is to take into
account the document frequency or the number of documents that a word occurs
in. In the case, we have the following metric.
![]()
Alternatively we can also consider
the collection frequency or the total number of occurrences in the corpus. The
idea being that certain important words will occur in every document, without
making them less informative (e.g. ‘earnings’ in earnings releases). A metric
based on this approach would be.
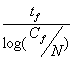
I did a subjective evaluation of
each of the metrics. Empirically, it appeared that taking the log of the term
frequency is not such a good idea when one is applying Principal Component
Analysis. My guess is that taking the log of the frequency is a non-linear
operation while PCA discovers linear variations in the data. I modified the document frequency as
follows.
![]()
As to whether it is better to
consider the collection frequency or the document frequency, the answer is that
it depended upon the data set. The problem with using collection frequency
being that the 1st principal component is likely a vector of “the’s,
and’s, but’s”. This is not unusual
since in the face recognition domain, the first eigenface is typically some
vague outline of a face. I went with the modified document frequency metric as
defined above (I will get back to this in the conclusion section).
There are other possible metrics, for example I could
weight terms according to the frequency of occurrence in a general corpus.
3.
Backprojection and singular values
Now
that we have found the common topics as n-dimensional vectors, how do we
extract out the topic keywords? First, we have determine which topic is the
main topic of the document. Commonly, composing a vector in terms of the
principal components is called backprojection. Since our principal components
or eigendocuments are all orthogonal vectors, this is easy to accomplish. Let E
be the matrix formed from the eigendocuments then vector p is the document
projected onto the eigenspace.
![]()
After
applying backprojection, this is the information we are left with:
1832.8053552111353
9445.57502599737
1402.6163078707768
4961.140314800185
-4058.618186618148
4628.4828148340675
933.6787396005402 4479.391563495432
788.5742390525835 4066.2998265214333
-481.42401396240757
3630.0927549701505
23.44096482441036 3416.7875917638235
Where
the numbers in the left column are the projected components in eigenspace, and
the numbers in the right column are the singular values. Some of the projected
values are negative because we are in essence ‘subtracting’ off the frequencies
of certain topics to arrive at the document frequencies. This seems unrealistic
and my approach has been to ignore the negative values.
If we divide the projected component
by the singular value we get a single number, the relevance of the topic.
Unfortunately, I have no formal justification for such an metric other than the
fact that the singular values are linear scaling factors. Such an metric tends
to favour the first eigendocument. This
is not an issue, if we consider a document as having several sub-topics rather
than a single topic. I will look into having more than one topic in the
evaluation section.
After selecting the main topic, we
now need the topic keywords. We simply take the eigendocument vector and select
the 20 words with highest weight. In this case, we would end up with the following
set of keywords:
buckley: 20.37403197873027
radomes: 20.37403197873027
intelligence: 19.26700141231
support: 14.48098796760573
bases: 13.58268798582018
campbell: 10.187015989365134
nmd: 10.187015989365134
government: 8.38797242217546
radio: 7.577049152548996
denver: 6.972903732217162
echelon: 6.79134399291009
trw: 6.79134399291009
navy: 6.79134399291009
classic: 6.79134399291009
wizard: 6.79134399291009
security: 6.725077458454946
nab: 6.4946135593277114
space: 6.493149076696486
stations: 6.326785290713001
national: 6.136668024398077
This
is a highly coherent set of keywords pertaining to national security and
government communications. The following is another set of keywords (taken from
the same dataset) that pertain to optical switching.
optical: 17.045206816644907
ofc: 9.021495664209564
ethernet: 7.1511080489416265
logic: 6.000554014920813
component: 4.770233274234911
crossconnect: 4.6415907289306375
adddrop: 4.6415907289306375
switches: 4.52523737920129
alloptical: 4.422167570242028
processing: 4.420466742703179
switching: 4.212264530038716
filters: 4.085637771912161
mux: 4.085637771912161
photonic: 3.9879840619783087
developers: 3.7260087031950886
anaheim: 3.656688375764404
density: 3.656688375764404
years: 3.55879050111118
startup: 3.5109361118305245
than: 3.441304395552341
Implementation
The system is implemented in Java and can be divided
into 3 modules corresponding to topic extraction, sentence extraction and
Bayesian classification. The topic extraction module reads in all of the files
from the corpus, extracting each word, and mapping the set of words to a set of
vector indicies. Then the corpus can be translated into a n*m matrix, where m
is the number of documents and n is the number of unique words in the corpus.
To find the set of unique words, it removes all numbers and converts to the
lower case but it doesn’t do any stemming.
It computes the SVD of the outer-product matrix to
find the ‘eigendocuments’ or the common topics of the corpus. Finally, it can
project the document vector onto the eigenspace, arriving at the main topic.
Note, all of the matrix operations like the SVD are implemented in a free
matrix package I downloaded off the web.
Doing sentence extraction is slightly more
complicated than extracting the unique words. The pattern it tries to match is (‘.’|’?’|’!’)(/s)(/s)*[A-Z,1-9].
This is not entirely correct, in particular an acronym like U. S. A would
constitute 2 sentence breaks. During the training phase approximately 4/80
training sentences were rejected due to an incorrect parsing of training files.
After each sentence has been extracted, it is stored in a data structure
(Sentence.java) that remembers it position in the paragraph.
For the summary-sentence classifier I implemented 4 features, the paragraph feature, the upper-case feature, the thematic-word feature and the topic-keyword feature. The thematic-word feature is found by converting the document into the same vector space as we did for PCA, and then extracting the components with the 20 highest weights. The upper-case feature is slightly trickier. We really want to find words that actually correspond to proper nouns. The approach is to find all upper-case words, not at the beginning of the sentence, which never occur as a lower case word in the entire corpus.
The classifier is just a CPD over the feature space.
During the training phase, each document with a corresponding training data
file, is read in and each sentence assignment with a feature vector. The
training file consists of 5 or 6 sentences which are to be included in the
summary. The CPD is updated to account for the training data. Finally, the
document to be summarized is read in. The sentences are ranked according the
probability of being in the summary and the sentences with the highest probability
are chosen.
To
run the program, you execute
Java summarize (k|f) filename
Where
k is with summarizing with topic keywords, so the feature set would be
(paragraph pos, upper-case feature, thematic-word feature, topic-keyword
feature), and f is summarizing without (pos, upper-case, thematic-word). Here
is some sample output.
0. (2,1) (0,1,1) The Spring Networld+Interop
confounded expectations by being one of the ... (0.7058823529411765)
1. (4,10) (2,1,1) We heard from every IC vendor in the
business that ... (0.35714285714285715)
2. (5,13) (2,1,1) We are talking about a time, perhaps two
years hence, ... (0.35714285714285715)
3.
(2,2) (1,1,1) The LAN market has indeed commoditized, and N+I has had ...
(0.3333333333333333)
4. (2,3) (2,0,0) It's hard to pinpoint what would account
for the N+I ... (0.2857142857142857)
Where
we are printing the feature vectors (e.g. (0,1,1)) and the associated
probability (0.70588).
Evaluation
I used the following dataset to evaluate the system,
a bi-weekly column discussing networking and telecom, in the online version of EE
times. For this data set, each
column was fairly short: a page of text with approx. 15-20 sentences each.
I created a dataset of 30 columns, all by the same author, taken over a 15-month period. Then I randomly chose 15 out of the 30 columns, summarized them, and put the results in training files. Finally for evaluation purposes I choose another 3 columns, randomly, out of the 15 remaining untrained documents.
To evaluate the system, I needed a objective way of
scoring the summaries. My approach was as follows, ask 3 people to read the 3
columns and summarize them by choosing 8 sentences from each document. Each
vote counts for a 1/3, the score for each sentence that is chosen, ranges from
1/3 to 1. I ask each person to choose 8 of 15-20 sentences because I want to
get a score distribution over a majority of the sentences. The top 5 sentences
from each computer-generated summary are then scored on this basis.
The following table summarizes the results of 3
different classifiers. The ‘Freq-only’ classifier used the following feature
vector: (paragraph pos, upper-case, thematic-word). The ‘Freq + Topic’
used (paragraph pos, upper-case, thematic-word, topic-keyword). ‘Topic1 + Topic2’ used the feature vector (paragraph
pos, upper-case, topic1-keyword, topic2-keyword) where we allow the
classifier to select a subtopic as well as the main topic.
|
|
Freq-only |
Freq+Topic |
Topic1
+ Topic2 |
|
Col
‘A’ |
3.333 |
3.666 |
3.666 |
|
Col
‘B’ |
2.666 |
2.666 |
3.000 |
|
Col
‘C’ |
1.666 |
2.333 |
2.333 |
All
the 3 classifiers did reasonably well on the tests. The numerical maximum of
the score is 5 but the actual maximum is less, since not all 3 people could
agree on 5 sentences. The actual maximum score was 4. So except for col ‘C’,
all 3 classifiers did quite well.
The results are pretty much in line
with expectations. The ‘Freq+Topic’ classifier should do slightly better than
‘Freq-only’ classifier since we have added information and increased the size
of feature space. Of course one concern when adding more features is that the
amount of training data has to be sufficiently large. Our 4-dimensional feature
space has 48 possible values and our training set has 80 data points. If we
were increase to 5-dimensional space with 96 possible values, then the 80
points would probably be insufficient.
Also the classifier that used only
topic keywords from 2 topics did slightly better than the ‘Freq+Topic’
classifier. This suggested that we would not need the most common words in the
article, only the keywords for the most common topics. To further validate this
fact, I tried testing each word-based feature independently, against the
training set.
|
Upper-Case |
162/264 |
|
Thematic-word |
180/264 |
|
Topic
1 |
174/264 |
|
Topic
2 |
160/264 |
The
results show that on an independent basis, the thematic-word feature did the
best of the word- based features. Of course this doesn’t rule out the fact that
‘topic 1’ and ‘topic 2’ could be inherently more compatible due to the fact
that they are derived from orthogonal basis vectors of the eigenspace. One can
not draw too many hard conclusions from the test results, because of the small
datasets involved. The overall sense I get, is that it is not easy to come up
with a single word-based feature which will outperform the frequency-based
thematic-word feature. However, it may be possible to compute a set of
word-based features such as the topic-keyword features, which together form a
superior classifier.
Conclusions
In this project, I found myself
tackling two problems: how to apply PCA to model the information content of a
corpus, and how to improve the trainable document summarizer (as outlined in
Kupeic ’95) by taking in account the relationship between a document and a
reference corpus. The process of applying PCA to a corpus is fairly tricky when
it comes to the problem of selecting a good vector space model.
The model I chose, which takes into account the term
frequency and the document frequency worked fairly well for the column dataset.
However, as I mentioned earlier it didn’t work well for earnings releases. I
tried applying PCA to a set of earnings reports and the fact ‘earnings’ is in
every document meant it didn’t show up as a topic keyword. Instead the system
produced very narrow keywords that didn’t seem to be about any topic, in
particular. Changing the model to take into account collection frequency
improved the keywords significantly. However, when this model was applied to
the column dataset, it produced a topic containing only ‘the’s’, ’and’s,
’but’s’, etc. A possibility may to be weight words according to their natural
frequency, as measured from a general corpus.
I found the quality of the components returned by
the PCA algorithm to be encouraging. They were not uniformly good, but it
certainly seemed that the system could identify a few important topics. Once
again, the topic vectors were very sensitive to the vector space model, which
also suggests that the datasets were too small: 30 documents are too few.
I am not that familiar with the literature in the
field of Information Retrieval, but most of the work I have seen focuses on
clustering the vector-space representation of documents, including papers from
Salton’s 1971 classic on IR [4]. Applying PCA to a corpus is fundamentally
different than clustering because we are breaking down the vectors and
constructing a new orthogonal basis, one that didn’t exist before.
As for the problem of improving the “training
document summarizer”, the biggest surprise is that the classifier already
performs quite well, without doing any sophisticated structural analysis. This
is partly due to the fact that the problem of ‘selecting summary sentences’ is
a not well-defined problem. On one column given to the 3 people for
summarization, where each were asked to choose approximately half of the
sentences, the union of the sentences they choose covered 16/17 sentences. It
would seem that the quality of a summary depends more on the coherence of the
sentences selected than the actual choice of sentences.
Adding a new feature that takes into account topic
keywords, seemed to improve performance. I believe the improvement would be
more visible for longer documents like earnings releases. I didn’t get around
to testing my hypothesis on the earning releases. On the surface it seemed to
be a significantly more difficult dataset (due to the length of the documents,
and the repeated use of canned and meaning-less phrases such as ‘Any forward
looking statements are purely speculative…’).
Also, I was only able to construct a very small testing
set. With such a small testing set, the results cannot be regarded as
statistically significant. My opinion (not just from the numeric data, but from
looking at the quality of the summaries) is that adding the topic-keyword
feature improved performance. While this feature doesn’t perform particularly
well when measured independently, it is possible that adding multiple features,
corresponding to multiple topics, can significantly improve performance.
However, this project has demonstrated that the more
important issue is how to generate readable and coherent summaries from the
summary sentences. In conclusion, in this project I have examined 2
sub-problems: using PCA to analyze a corpus of documents and improving the
performance of summary sentence selection. I think PCA is a technique that is
applicable to document corpus analysis. Furthermore, the relationship between a
document and its corpus is relevant to the problem of summary sentence
selection. It can improve performance, although it is not clear by how much.
References
[1]
Julian Kupeic, Jan Pedersen, and Francine Chen. 1995. A Trainable Document
Summarizer. In Proceedings of ACM-SIGIR ’95. Seattle, WA.
[2]
Regina Barzilay, Kathleen R. McKeown, and Michael Elhadad, 1999. Information
fusion in the context of multi-document summarization. In Proceedings of the
37 Annual Meeting of the ACL.
[3]
Dragomir R. Radev and Kathleen R. McKeown. 1998. Generating natural language
summaries from multiple on-line sources. Computational Linguistics,
24(3):469-500.
[4]
Gerald Salton. The Smart Retrieval System, 1971. Prentice Hall,
Englewood Cliffs, N.J.