The Bernoulli model

There are two different ways we can set up an NB classifier. The model we introduced in the previous section is the multinomial model . It generates one term from the vocabulary in each position of the document, where we assume a generative model that will be discussed in more detail in Section 13.4 (see also page 12.1.1 ).

An alternative to the multinomial model is the multivariate Bernoulli model or Bernoulli model . It is equivalent to the binary independence model of Section 11.3 (page ), which generates an indicator for each term of the vocabulary, either $1$ indicating presence of the term in the document or $0$ indicating absence. Figure 13.3 presents training and testing algorithms for the Bernoulli model. The Bernoulli model has the same time complexity as the multinomial model.

The different generation models imply different estimation strategies and different classification rules. The Bernoulli model estimates $\hat{P}(\tcword\vert\tcjclass)$ as the fraction of documents of class $\tcjclass$ that contain term $\tcword$ (Figure 13.3 , TRAINBERNOULLINB, line 8). In contrast, the multinomial model estimates $\hat{P}(\tcword\vert\tcjclass)$ as the fraction of tokens or fraction of positions in documents of class $\tcjclass$ that contain term $\tcword$ (Equation 119). When classifying a test document, the Bernoulli model uses binary occurrence information, ignoring the number of occurrences, whereas the multinomial model keeps track of multiple occurrences. As a result, the Bernoulli model typically makes many mistakes when classifying long documents. For example, it may assign an entire book to the class China because of a single occurrence of the term China.

The models also differ in how nonoccurring terms are used in classification. They do not affect the classification decision in the multinomial model; but in the Bernoulli model the probability of nonoccurrence is factored in when computing $P(c\vert d)$ (Figure 13.3 , APPLYBERNOULLINB, Line 7). This is because only the Bernoulli NB model models absence of terms explicitly.

Worked example. Applying the Bernoulli model to the example in Table 13.1 , we have the same estimates for the priors as before: $\hat{P}(c) = 3/4$, $\hat{P}(\overline{c}) = 1/4$. The conditional probabilities are:

$$\begin{eqnarray*} \hat{P}(\term{Chinese}\vert c)&=& (3+1)/(3+2) = 4/5\\ \hat{P}... ... \hat{P}(\term{Shanghai}\vert\overline{c}) &=& (0+1)/(1+2) = 1/3 \end{eqnarray*}$$

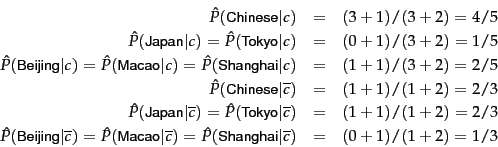
The denominators are $(3+2)$ and $(1+2)$ because there are three documents in $c$ and one document in $\overline{c}$ and because the constant $B$ in Equation 119 is 2 - there are two cases to consider for each term, occurrence and nonoccurrence.

The scores of the test document for the two classes are

$$\begin{eqnarray*} \hat{P}(c\vert d_5) &\propto& \hat{P}(c) \cdot \hat{P}(\term{C... ...!2/5) \cdot (1\! - \!2/5) \cdot (1\! - \!2/5)\\ &\approx& 0.005 \end{eqnarray*}$$

and, analogously,

$$\begin{eqnarray*} \hat{P}(\overline{c}\vert d_5) &\propto& 1/4 \cdot 2/3 \cdot 2... ...!1/3) \cdot (1\! - \!1/3) \cdot (1\! - \!1/3)\\ &\approx& 0.022 \end{eqnarray*}$$

Thus, the classifier assigns the test document to $\overline{c} =$ not-China. When looking only at binary occurrence and not at term frequency, Japan and Tokyo are indicators for $\overline{c}$ ($2/3>1/5$) and the conditional probabilities of Chinese for $c$ and $\overline{c}$ are not different enough (4/5 vs. 2/3) to affect the classification decision. End worked example.