




Next: Tf-idf weighting
Up: Term frequency and weighting
Previous: Term frequency and weighting
Contents
Index
Inverse document frequency
Raw term frequency as above suffers from a critical problem: all terms are considered equally important when it comes to assessing relevancy on a query. In fact certain terms have little or no discriminating power in determining relevance. For instance, a collection of documents on the auto industry is likely to have the term auto in almost every document. To this end, we introduce a mechanism for attenuating the effect of terms that occur too often in the collection to be meaningful for relevance determination. An immediate idea is to scale down the term weights of terms with high collection frequency, defined to be the total number of occurrences of a term in the collection. The idea would be to reduce the 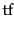 weight of a term by a factor that grows with its collection frequency.
weight of a term by a factor that grows with its collection frequency.
Instead, it is more commonplace to use for this purpose the document frequency 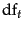 , defined to be the number of documents in the collection that contain a term
, defined to be the number of documents in the collection that contain a term 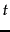 . This is because in trying to discriminate between documents for the purpose of scoring it is better to use a document-level statistic (such as the number of documents containing a term) than to use a collection-wide statistic for the term.
. This is because in trying to discriminate between documents for the purpose of scoring it is better to use a document-level statistic (such as the number of documents containing a term) than to use a collection-wide statistic for the term.
Figure 6.7:
Collection frequency (cf) and document frequency (df) behave differently, as in this example from the Reuters collection.
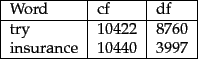 |
The reason to prefer df to cf is illustrated in Figure 6.7 , where a simple example shows that collection frequency (cf) and document frequency (df) can behave rather differently. In particular, the cf values for both try and insurance are roughly equal, but their df values differ significantly. Intuitively, we want the few documents that contain insurance to get a higher boost for a query on insurance than the many documents containing try get from a query on try.
How is the document frequency df of a term used to scale its weight? Denoting as usual the total number of documents in a collection by 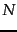 , we define the inverse document frequency of a term
, we define the inverse document frequency of a term 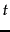 as follows:
as follows:
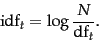 |
(21) |
Thus the idf of a rare term is high, whereas the idf of a
frequent term is likely to be low. Figure 6.8 gives
an example of idf's in the Reuters collection of 806,791
documents; in this example logarithms are to the base 10. In
fact, as we will see in Exercise 6.2.2 , the precise
base of the logarithm is not material to ranking. We will give
on page 11.3.3 a justification of the
particular form in Equation 21.





Next: Tf-idf weighting
Up: Term frequency and weighting
Previous: Term frequency and weighting
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() , defined to be the number of documents in the collection that contain a term
, defined to be the number of documents in the collection that contain a term ![]() . This is because in trying to discriminate between documents for the purpose of scoring it is better to use a document-level statistic (such as the number of documents containing a term) than to use a collection-wide statistic for the term.
. This is because in trying to discriminate between documents for the purpose of scoring it is better to use a document-level statistic (such as the number of documents containing a term) than to use a collection-wide statistic for the term.
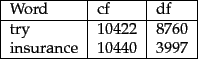
![]() , we define the inverse document frequency of a term
, we define the inverse document frequency of a term ![]() as follows:
as follows: