Result ranking by machine learning

The above ideas can be readily generalized to functions of many more than two variables. There are lots of other scores that are indicative of the relevance of a document to a query, including static quality (PageRank-style measures, discussed in Chapter 21 ), document age, zone contributions, document length, and so on. Providing that these measures can be calculated for a training document collection with relevance judgments, any number of such measures can be used to train a machine learning classifier. For instance, we could train an SVM over binary relevance judgments, and order documents based on their probability of relevance, which is monotonic with the documents' signed distance from the decision boundary.

However, approaching IR result ranking like this is not necessarily the right way to think about the problem. Statisticians normally first divide problems into classification problems (where a categorical variable is predicted) versus regression problems (where a real number is predicted). In between is the specialized field of ordinal regression where a ranking is predicted. Machine learning for ad hoc retrieval is most properly thought of as an ordinal regression problem, where the goal is to rank a set of documents for a query, given training data of the same sort. This formulation gives some additional power, since documents can be evaluated relative to other candidate documents for the same query, rather than having to be mapped to a global scale of goodness, while also weakening the problem space, since just a ranking is required rather than an absolute measure of relevance. Issues of ranking are especially germane in web search, where the ranking at the very top of the results list is exceedingly important, whereas decisions of relevance of a document to a query may be much less important. Such work can and has been pursued using the structural SVM framework which we mentioned in Section 15.2.2 , where the class being predicted is a ranking of results for a query, but here we will present the slightly simpler ranking SVM.

The construction of a ranking SVM proceeds as follows. We begin with a set of judged queries. For each training query $q$, we have a set of documents returned in response to the query, which have been totally ordered by a person for relevance to the query. We construct a vector of features $\psi_j = \psi(d_j, q)$ for each document/query pair, using features such as those discussed in Section 15.4.1 , and many more. For two documents $d_i$ and $d_j$, we then form the vector of feature differences:

$$\Phi(d_i, d_j, q) = \psi(d_i, q) - \psi(d_j, q)$$ (180)

By hypothesis, one of $d_i$ and $d_j$ has been judged more relevant. If $d_i$ is judged more relevant than $d_j$, denoted $d_i \prec d_j$ ($d_i$ should precede $d_j$ in the results ordering), then we will assign the vector $\Phi(d_i, d_j, q)$ the class $y_{ijq} = +1$; otherwise $-1$. The goal then is to build a classifier which will return

$$\vec{w}^{T}\Phi(d_i, d_j, q) > 0 \mbox{\quad iff\quad} d_i \prec d_j$$ (181)

This SVM learning task is formalized in a manner much like the other examples that we saw before:

We can leave out $y_{ijq}$ in the statement of the constraint, since we only need to consider the constraint for document pairs ordered in one direction, since $\prec$ is antisymmetric. These constraints are then solved, as before, to give a linear classifier which can rank pairs of documents. This approach has been used to build ranking functions which outperform standard hand-built ranking functions in IR evaluations on standard data sets; see the references for papers that present such results.

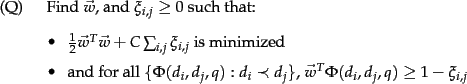
Both of the methods that we have just looked at use a linear weighting of document features that are indicators of relevance, as has most work in this area. It is therefore perhaps interesting to note that much of traditional IR weighting involves nonlinear scaling of basic measurements (such as log-weighting of term frequency, or idf). At the present time, machine learning is very good at producing optimal weights for features in a linear combination (or other similar restricted model classes), but it is not good at coming up with good nonlinear scalings of basic measurements. This area remains the domain of human feature engineering.

The idea of learning ranking functions has been around for a number of years, but it is only very recently that sufficient machine learning knowledge, training document collections, and computational power have come together to make this method practical and exciting. It is thus too early to write something definitive on machine learning approaches to ranking in information retrieval, but there is every reason to expect the use and importance of machine learned ranking approaches to grow over time. While skilled humans can do a very good job at defining ranking functions by hand, hand tuning is difficult, and it has to be done again for each new document collection and class of users.

Exercises.

• Plot the first 7 rows of Table 15.3 in the $\alpha$-$\omega$ plane to produce a figure like that in Figure 15.7 .

• Write down the equation of a line in the $\alpha$-$\omega$ plane separating the Rs from the Ns.

• Give a training example (consisting of values for $\alpha, \omega$ and the relevance judgment) that when added to the training set makes it impossible to separate the R's from the N's using a line in the $\alpha$-$\omega$ plane.