




Next: The Binary Independence Model
Up: The Probability Ranking Principle
Previous: The 1/0 loss case
Contents
Index
Suppose, instead, that we assume a model
of retrieval costs. Let 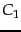 be the cost of not retrieving
a relevant document and
be the cost of not retrieving
a relevant document and 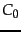 the cost of retrieval of a
nonrelevant document. Then the Probability Ranking
Principle says that
if for a specific document
the cost of retrieval of a
nonrelevant document. Then the Probability Ranking
Principle says that
if for a specific document 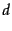 and
for all documents
and
for all documents 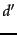 not yet retrieved
not yet retrieved
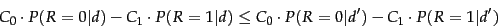 |
(62) |
then 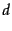 is the next document to be retrieved. Such a model gives a formal framework where we can model differential costs of false positives and false negatives and even system performance issues at the modeling stage, rather than simply at the evaluation stage, as we did in Section 8.6 (page
is the next document to be retrieved. Such a model gives a formal framework where we can model differential costs of false positives and false negatives and even system performance issues at the modeling stage, rather than simply at the evaluation stage, as we did in Section 8.6 (page ![[*]](http://nlp.stanford.edu/IR-book/html/icons/crossref.png) ). However, we will not further consider loss/utility models in this chapter.
). However, we will not further consider loss/utility models in this chapter.
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() be the cost of not retrieving
a relevant document and
be the cost of not retrieving
a relevant document and ![]() the cost of retrieval of a
nonrelevant document. Then the Probability Ranking
Principle says that
if for a specific document
the cost of retrieval of a
nonrelevant document. Then the Probability Ranking
Principle says that
if for a specific document ![]() and
for all documents
and
for all documents ![]() not yet retrieved
not yet retrieved