 |
In Section 6.3.1 we normalized each document vector by the Euclidean length of the vector, so that all document vectors turned into unit vectors. In doing so, we eliminated all information on the length of the original document; this masks some subtleties about longer documents. First, longer documents will - as a result of containing more terms - have higher tf values. Second, longer documents contain more distinct terms. These factors can conspire to raise the scores of longer documents, which (at least for some information needs) is unnatural. Longer documents can broadly be lumped into two categories: (1) verbose documents that essentially repeat the same content - in these, the length of the document does not alter the relative weights of different terms; (2) documents covering multiple different topics, in which the search terms probably match small segments of the document but not all of it - in this case, the relative weights of terms are quite different from a single short document that matches the query terms. Compensating for this phenomenon is a form of document length normalization that is independent of term and document frequencies. To this end, we introduce a form of normalizing the vector representations of documents in the collection, so that the resulting ``normalized'' documents are not necessarily of unit length. Then, when we compute the dot product score between a (unit) query vector and such a normalized document, the score is skewed to account for the effect of document length on relevance. This form of compensation for document length is known as pivoted document length normalization .
Consider a document collection together with an ensemble of queries for that collection. Suppose that we were given, for each query ![]() and for each document
and for each document ![]() , a Boolean judgment of whether or not
, a Boolean judgment of whether or not ![]() is relevant to the query
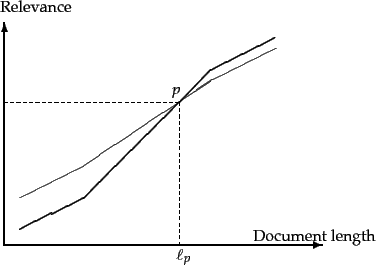
is relevant to the query ![]() ; in Chapter 8 we will see how to procure such a set of relevance judgments for a query ensemble and a document collection. Given this set of relevance judgments, we may compute a probability of relevance as a function of document length, averaged over all queries in the ensemble. The resulting plot may look like the curve drawn in thick lines in Figure 6.16 . To compute this curve, we bucket documents by length and compute the fraction of relevant documents in each bucket, then plot this fraction against the median document length of each bucket. (Thus even though the ``curve'' in Figure 6.16 appears to be continuous, it is in fact a histogram of discrete buckets of document length.)
; in Chapter 8 we will see how to procure such a set of relevance judgments for a query ensemble and a document collection. Given this set of relevance judgments, we may compute a probability of relevance as a function of document length, averaged over all queries in the ensemble. The resulting plot may look like the curve drawn in thick lines in Figure 6.16 . To compute this curve, we bucket documents by length and compute the fraction of relevant documents in each bucket, then plot this fraction against the median document length of each bucket. (Thus even though the ``curve'' in Figure 6.16 appears to be continuous, it is in fact a histogram of discrete buckets of document length.)
On the other hand, the curve in thin lines shows what might happen with the same documents and query ensemble if we were to use relevance as prescribed by cosine normalization Equation 27 - thus, cosine normalization has a tendency to distort the computed relevance vis-à-vis the true relevance, at the expense of longer documents. The thin and thick curves crossover at a point ![]() corresponding to document length
corresponding to document length ![]() , which we refer to as the pivot length; dashed lines mark this point on the
, which we refer to as the pivot length; dashed lines mark this point on the ![]() and
and ![]() axes. The idea of pivoted document length normalization would then be to ``rotate'' the cosine normalization curve counter-clockwise about
axes. The idea of pivoted document length normalization would then be to ``rotate'' the cosine normalization curve counter-clockwise about ![]() so that it more closely matches thick line representing the relevance vs. document length curve. As mentioned at the beginning of this section, we do so by using in Equation 27 a normalization factor for each document vector
so that it more closely matches thick line representing the relevance vs. document length curve. As mentioned at the beginning of this section, we do so by using in Equation 27 a normalization factor for each document vector ![]() that is not the Euclidean length of that vector, but instead one that is larger than the Euclidean length for documents of length less than
that is not the Euclidean length of that vector, but instead one that is larger than the Euclidean length for documents of length less than ![]() , and smaller for longer documents.
, and smaller for longer documents.
To this end, we first note that the normalizing term for ![]() in the denominator of Equation 27 is its Euclidean length, denoted
in the denominator of Equation 27 is its Euclidean length, denoted ![]() . In the simplest implementation of pivoted document length normalization, we use a normalization factor in the denominator that is linear in
. In the simplest implementation of pivoted document length normalization, we use a normalization factor in the denominator that is linear in ![]() , but one of slope
, but one of slope ![]() as in Figure 6.17 . In this figure, the
as in Figure 6.17 . In this figure, the ![]() axis represents
axis represents ![]() , while the
, while the ![]() axis represents possible normalization factors we can use. The thin line
axis represents possible normalization factors we can use. The thin line ![]() depicts the use of cosine normalization. Notice the following aspects of the thick line representing pivoted length normalization:
depicts the use of cosine normalization. Notice the following aspects of the thick line representing pivoted length normalization:
| (32) |
Of course, pivoted document length normalization is not appropriate for all applications. For instance, in a collection of answers to frequently asked questions (say, at a customer service website), relevance may have little to do with document length. In other cases the dependency may be more complex than can be accounted for by a simple linear pivoted normalization. In such cases, document length can be used as a feature in the machine learning based scoring approach of Section 6.1.2 .
Exercises.
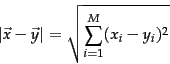 |
(33) |
| ||||||||||||||||||||||||||||||||||||||||||||||||||