




Next: Components of an information
Up: Efficient scoring and ranking
Previous: Impact ordering
Contents
Index
Cluster pruning
In cluster pruning we have a preprocessing step during which we cluster the document vectors. Then at query time, we consider only documents in a small number of clusters as candidates for which we compute cosine scores. Specifically, the preprocessing step is as follows:
- Pick
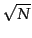 documents at random from the collection. Call these leaders.
documents at random from the collection. Call these leaders.
- For each document that is not a leader, we compute its nearest leader.
We refer to documents that are not leaders as followers. Intuitively, in the partition of the followers induced by the use of 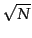 randomly chosen leaders, the expected number of followers for each leader is
randomly chosen leaders, the expected number of followers for each leader is
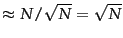 .
Next, query processing proceeds as follows:
.
Next, query processing proceeds as follows:
- Given a query
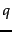 , find the leader
, find the leader 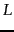 that is closest to
that is closest to 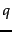 . This entails computing cosine similarities from
. This entails computing cosine similarities from 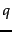 to each of the
to each of the 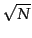 leaders.
leaders.
- The candidate set
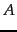 consists of
consists of 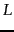 together with its followers. We compute the cosine scores for all documents in this candidate set.
together with its followers. We compute the cosine scores for all documents in this candidate set.
The use of randomly chosen leaders for clustering is fast and likely to reflect the distribution of the document vectors in the vector space: a region of the vector space that is dense in documents is likely to produce multiple leaders and thus a finer partition into sub-regions. This illustrated in Figure 7.3 .
Figure 7.3:
Cluster pruning.
![\includegraphics[width=8cm]{clusterpruning.eps}](img499.png) |
Variations of cluster pruning introduce additional parameters 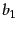 and
and 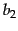 , both of which are positive integers. In the pre-processing step we attach each follower to its
, both of which are positive integers. In the pre-processing step we attach each follower to its 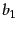 closest leaders, rather than a single closest leader. At query time we consider the
closest leaders, rather than a single closest leader. At query time we consider the 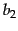 leaders closest to the query
leaders closest to the query 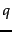 . Clearly, the basic scheme above corresponds to the case
. Clearly, the basic scheme above corresponds to the case 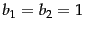 . Further, increasing
. Further, increasing 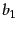 or
or 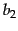 increases the likelihood of finding
increases the likelihood of finding 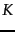 documents that are more likely to be in the set of true top-scoring
documents that are more likely to be in the set of true top-scoring 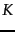 documents, at the expense of more computation. We reiterate this approach when describing clustering in Chapter 16 (page 16.1 ).
documents, at the expense of more computation. We reiterate this approach when describing clustering in Chapter 16 (page 16.1 ).
Exercises.
- We suggested above (Figure 7.2 ) that the postings
for static quality ordering be in decreasing order of
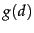 . Why do we use the decreasing rather than the
increasing order?
. Why do we use the decreasing rather than the
increasing order?
- When discussing champion lists, we simply used the
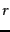 documents with the largest tf values to create the champion list for
documents with the largest tf values to create the champion list for 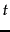 . But when considering global champion lists, we used idf as well, identifying documents with the largest values of
. But when considering global champion lists, we used idf as well, identifying documents with the largest values of
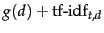 . Why do we differentiate between these two cases?
. Why do we differentiate between these two cases?
- If we were to only have one-term queries, explain
why the use of global champion lists with
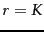 suffices for
identifying the
suffices for
identifying the 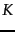 highest scoring documents. What is a
simple modification to this idea if we were to only have
highest scoring documents. What is a
simple modification to this idea if we were to only have
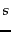 -term queries for any fixed integer
-term queries for any fixed integer 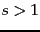 ?
?
- Explain how the common global ordering by
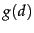 values in all high and low lists helps make the score computation efficient.
values in all high and low lists helps make the score computation efficient.
- Consider again the data of Exercise 6.4.4 with nnn.atc for the query-dependent scoring. Suppose that we were given static quality scores of 1 for Doc1 and 2 for Doc2. Determine under Equation 35 what ranges of static quality score for Doc3 result in it being the first, second or third result for the query best car insurance.
- Sketch the frequency-ordered postings for the data in Figure 6.9 .
- Let the static quality scores for Doc1, Doc2 and Doc3 in Figure 6.11 be respectively 0.25, 0.5 and 1. Sketch the postings for impact ordering when each postings list is ordered by the sum of the static quality score and the Euclidean normalized tf values in Figure 6.11 .
- The nearest-neighbor problem in the plane is the following: given a set of
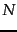 data points on the plane, we preprocess them into some data structure such that, given a query point
data points on the plane, we preprocess them into some data structure such that, given a query point 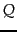 , we seek the point in
, we seek the point in 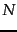 that is closest to
that is closest to 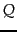 in Euclidean distance. Clearly cluster pruning can be used as an approach to the nearest-neighbor problem in the plane, if we wished to avoid computing the distance from
in Euclidean distance. Clearly cluster pruning can be used as an approach to the nearest-neighbor problem in the plane, if we wished to avoid computing the distance from 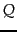 to every one of the query points. Devise a simple example on the plane so that with two leaders, the answer returned by cluster pruning is incorrect (it is not the data point closest to
to every one of the query points. Devise a simple example on the plane so that with two leaders, the answer returned by cluster pruning is incorrect (it is not the data point closest to 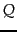 ).
).





Next: Components of an information
Up: Efficient scoring and ranking
Previous: Impact ordering
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() and
and ![]() , both of which are positive integers. In the pre-processing step we attach each follower to its
, both of which are positive integers. In the pre-processing step we attach each follower to its ![]() closest leaders, rather than a single closest leader. At query time we consider the
closest leaders, rather than a single closest leader. At query time we consider the ![]() leaders closest to the query
leaders closest to the query ![]() . Clearly, the basic scheme above corresponds to the case
. Clearly, the basic scheme above corresponds to the case ![]() . Further, increasing
. Further, increasing ![]() or
or ![]() increases the likelihood of finding
increases the likelihood of finding ![]() documents that are more likely to be in the set of true top-scoring
documents that are more likely to be in the set of true top-scoring ![]() documents, at the expense of more computation. We reiterate this approach when describing clustering in Chapter 16 (page 16.1 ).
documents, at the expense of more computation. We reiterate this approach when describing clustering in Chapter 16 (page 16.1 ).