




Next: References and further reading
Up: Positional postings and phrase
Previous: Positional index size.
Contents
Index
The strategies of biword indexes and positional indexes can be
fruitfully combined. If users commonly query on particular phrases,
such as Michael Jackson, it is quite inefficient to keep merging
positional postings lists. A combination strategy uses a phrase index,
or just a biword index ,
for certain queries and uses a positional index
for other phrase queries. Good queries to include in the phrase index
are ones known to be common based on recent querying behavior.
But this is not the only criterion: the most expensive phrase queries
to evaluate are ones where the individual words are common but the
desired phrase is comparatively rare. Adding Britney Spears as a
phrase index entry may only give a speedup factor to that query of about
3, since most documents that mention either word are valid results,
whereas adding The Who as a phrase index entry may
speed up that query by a factor of 1000. Hence, having the latter is
more desirable, even if it is a relatively less common query.
Williams et al. (2004) evaluate an even more
sophisticated scheme which employs indexes of both these sorts and
additionally a partial next word index as a halfway house between the first
two strategies. For each term, a next word index records terms
that follow it in a document. They conclude that such a strategy allows a typical
mixture of web phrase queries to be completed in one quarter of the time
taken by use of a positional index alone, while taking up 26% more
space than use of a positional index alone.
Exercises.
- Assume a biword index. Give an example of a document which will be returned for
a query of New York University but is actually a false positive which should not be returned.
- Shown below is a portion of a positional index in the format:
term: doc1:
 position1, position2, ...
position1, position2, ... ; doc2:
; doc2:  position1, position2, ...
position1, position2, ... ; etc.
; etc.
angels: 2:  36,174,252,651
36,174,252,651 ; 4:
; 4:  12,22,102,432
12,22,102,432 ; 7:
; 7:  17
17 ;
;
fools: 2:  1,17,74,222
1,17,74,222 ; 4:
; 4:  8,78,108,458
8,78,108,458 ; 7:
; 7:  3,13,23,193
3,13,23,193 ;
;
fear: 2:  87,704,722,901
87,704,722,901 ; 4:
; 4:  13,43,113,433
13,43,113,433 ; 7:
; 7:  18,328,528
18,328,528 ;
;
in: 2:  3,37,76,444,851
3,37,76,444,851 ; 4:
; 4:  10,20,110,470,500
10,20,110,470,500 ; 7:
; 7:  5,15,25,195
5,15,25,195 ;
;
rush: 2:  2,66,194,321,702
2,66,194,321,702 ; 4:
; 4:  9,69,149,429,569
9,69,149,429,569 ; 7:
; 7:  4,14,404
4,14,404 ;
;
to: 2:  47,86,234,999
47,86,234,999 ; 4:
; 4:  14,24,774,944
14,24,774,944 ; 7:
; 7:  199,319,599,709
199,319,599,709 ;
;
tread: 2:  57,94,333
57,94,333 ; 4:
; 4:  15,35,155
15,35,155 ; 7:
; 7:  20,320
20,320 ;
;
where: 2:  67,124,393,1001
67,124,393,1001 ; 4:
; 4:  11,41,101,421,431
11,41,101,421,431 ; 7:
; 7:  16,36,736
16,36,736 ;
;
Which document(s) if any match each of the following queries, where each
expression within
quotes is a phrase query?
- ``fools rush in''
- ``fools rush in'' AND ``angels fear to tread''
- Consider the following fragment of a positional index with
the format:
word: document:  position, position,
position, position, 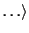 ; document:
; document:  position,
position, 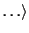
...
Gates: 1:  3
3 ; 2:
; 2:  6
6 ; 3:
; 3:  2,17
2,17 ; 4:
; 4:  1
1 ;
;
IBM: 4:  3
3 ; 7:
; 7:  14
14 ;
;
Microsoft: 1:  1
1 ; 2:
; 2:  1,21
1,21 ; 3:
; 3:  3
3 ; 5:
; 5:  16,22,51
16,22,51 ;
;
The / operator, word1 /
operator, word1 / word2 finds occurrences of
word1 within
word2 finds occurrences of
word1 within  words of
word2 (on either side), where
words of
word2 (on either side), where  is a positive integer
argument. Thus
is a positive integer
argument. Thus 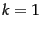 demands that word1 be adjacent to
word2.
demands that word1 be adjacent to
word2.
- Describe the set of documents that satisfy the query Gates /2
Microsoft.
- Describe each set of values for
 for which the query Gates /
for which the query Gates / Microsoft returns a different set of documents as the answer.
Microsoft returns a different set of documents as the answer.
- Consider the general procedure for merging two
positional postings lists for a given document, to determine the document positions
where a document satisfies a /
 clause (in general there can be multiple positions
at which each term occurs in a single
document). We begin with a pointer to the
position of occurrence of each term and move each pointer along the list
of occurrences in the document, checking as
we do so whether we have a hit for /
clause (in general there can be multiple positions
at which each term occurs in a single
document). We begin with a pointer to the
position of occurrence of each term and move each pointer along the list
of occurrences in the document, checking as
we do so whether we have a hit for / . Each move of either pointer
counts as a step. Let
. Each move of either pointer
counts as a step. Let 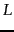 denote the total
number of occurrences of the two terms in the document. What is the big-O
complexity of the merge procedure, if we
wish to have postings including positions in the result?
denote the total
number of occurrences of the two terms in the document. What is the big-O
complexity of the merge procedure, if we
wish to have postings including positions in the result?
- Consider the adaptation of the basic algorithm for intersection of two postings
lists postings-merge-algorithm to the one in
Figure 2.12 (page
![[*]](http://nlp.stanford.edu/IR-book/html/icons/crossref.png) ), which handles proximity
queries.
A naive algorithm for this operation could be
), which handles proximity
queries.
A naive algorithm for this operation could be
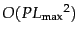 , where
, where 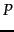 is the sum of the lengths of the postings lists (i.e., the sum of document
frequencies) and
is the sum of the lengths of the postings lists (i.e., the sum of document
frequencies) and 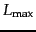 is the maximum length of a document (in tokens).
is the maximum length of a document (in tokens).
- Go through this algorithm carefully and explain how it works.
- What is the complexity of this algorithm? Justify your answer carefully.
- For certain queries and data distributions, would another algorithm be
more efficient? What complexity does it have?
- Suppose we wish to use a postings intersection procedure
to determine simply the list of documents that satisfy
a /
 clause, rather than returning the list of positions,
as in Figure 2.12 (page
clause, rather than returning the list of positions,
as in Figure 2.12 (page ![[*]](http://nlp.stanford.edu/IR-book/html/icons/crossref.png) ).
For simplicity, assume
).
For simplicity, assume 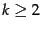 .
Let
.
Let 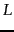 denote the total
number of occurrences of the two terms in the document collection
(i.e., the sum of their collection frequencies).
Which of the following is true? Justify your answer.
denote the total
number of occurrences of the two terms in the document collection
(i.e., the sum of their collection frequencies).
Which of the following is true? Justify your answer.
- The merge can be accomplished in a number of steps linear in
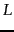 and independent of
and independent of  , and we can ensure that each
pointer moves only to the right.
, and we can ensure that each
pointer moves only to the right.
- The merge can be accomplished in a
number of steps
linear in
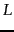 and independent of
and independent of  , but a pointer may be forced to
move non-monotonically (i.e., to sometimes back up)
, but a pointer may be forced to
move non-monotonically (i.e., to sometimes back up)
- The merge can require
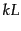 steps in some cases.
steps in some cases.
- How could an IR system combine use of a positional index and use of stop words?
What is the potential problem, and how could it be handled?





Next: References and further reading
Up: Positional postings and phrase
Previous: Positional index size.
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
36,174,252,651
; 4:
12,22,102,432
; 7:
17
;
1,17,74,222
; 4:
8,78,108,458
; 7:
3,13,23,193
;
87,704,722,901
; 4:
13,43,113,433
; 7:
18,328,528
;
3,37,76,444,851
; 4:
10,20,110,470,500
; 7:
5,15,25,195
;
2,66,194,321,702
; 4:
9,69,149,429,569
; 7:
4,14,404
;
47,86,234,999
; 4:
14,24,774,944
; 7:
199,319,599,709
;
57,94,333
; 4:
15,35,155
; 7:
20,320
;
67,124,393,1001
; 4:
11,41,101,421,431
; 7:
16,36,736
;
position, position,
; document:
position,
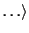
3
; 2:
6
; 3:
2,17
; 4:
1
;
3
; 7:
14
;
1
; 2:
1,21
; 3:
3
; 5:
16,22,51
;
 for which the query Gates /
for which the query Gates / Microsoft returns a different set of documents as the answer.
Microsoft returns a different set of documents as the answer.
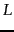 and independent of
and independent of  , and we can ensure that each
pointer moves only to the right.
, and we can ensure that each
pointer moves only to the right.
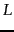 and independent of
and independent of  , but a pointer may be forced to
move non-monotonically (i.e., to sometimes back up)
, but a pointer may be forced to
move non-monotonically (i.e., to sometimes back up)
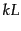 steps in some cases.
steps in some cases.