As in Chapter 6 , we represent documents as
vectors in
![]() in this chapter. To illustrate properties
of document vectors in vector classification,
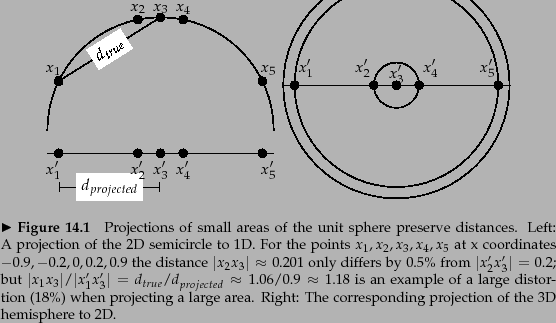
we will render these vectors as points in a plane as in the
example in Figure 14.1 . In
reality, document vectors are length-normalized
unit vectors that point to the surface of a hypersphere. We
can view the 2D planes in our figures as projections onto a
plane of the surface of a (hyper-)sphere as shown in
Figure 14.2 . Distances on the surface of the sphere
and on the projection plane are approximately the same as
long as we restrict ourselves to small areas of the surface
and choose an appropriate projection
(Exercise 14.1 ).
in this chapter. To illustrate properties
of document vectors in vector classification,
we will render these vectors as points in a plane as in the
example in Figure 14.1 . In
reality, document vectors are length-normalized
unit vectors that point to the surface of a hypersphere. We
can view the 2D planes in our figures as projections onto a
plane of the surface of a (hyper-)sphere as shown in
Figure 14.2 . Distances on the surface of the sphere
and on the projection plane are approximately the same as
long as we restrict ourselves to small areas of the surface
and choose an appropriate projection
(Exercise 14.1 ).
Decisions of many vector space classifiers are
based on a notion of distance, e.g., when computing the nearest
neighbors in kNN classification.
We will use Euclidean
distance in this chapter as the underlying distance measure.
We observed earlier (Exercise 6.4.4 ,
page ![]() ) that there is a direct
correspondence between cosine similarity and Euclidean
distance for length-normalized vectors. In vector space classification, it
rarely matters whether the relatedness of two documents is
expressed in terms of similarity or distance.
) that there is a direct
correspondence between cosine similarity and Euclidean
distance for length-normalized vectors. In vector space classification, it
rarely matters whether the relatedness of two documents is
expressed in terms of similarity or distance.
However, in addition to documents, centroids or averages of vectors also play an important role in vector space classification. Centroids are not length-normalized. For unnormalized vectors, dot product, cosine similarity and Euclidean distance all have different behavior in general (Exercise 14.8 ). We will be mostly concerned with small local regions when computing the similarity between a document and a centroid, and the smaller the region the more similar the behavior of the three measures is.
Exercises.