




Next: Zipf's law: Modeling the
Up: Statistical properties of terms
Previous: Statistical properties of terms
Contents
Index
![\includegraphics[width=9cm]{art/heapsmall.eps}](img236.png)
Heaps' law.Vocabulary size
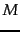
as a function of
collection size
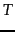
(number of tokens) for Reuters-RCV1.
For these data, the dashed line
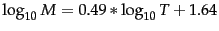
is the best least-squares fit. Thus,
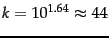
and
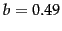
.
A better way of getting a handle on 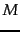 is Heaps'
law , which
estimates vocabulary size as a function of collection size:
is Heaps'
law , which
estimates vocabulary size as a function of collection size:
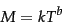 |
(1) |
where 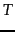 is the number of tokens in the collection. Typical
values for the parameters
is the number of tokens in the collection. Typical
values for the parameters  and
and 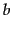 are:
are:
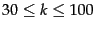 and
and 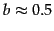 .
The motivation for Heaps' law is that the simplest possible
relationship between collection size and vocabulary size is linear in log-log space
and the assumption of linearity is usually born out in
practice as shown in Figure 5.1 for Reuters-RCV1.
In this case, the fit is excellent for
.
The motivation for Heaps' law is that the simplest possible
relationship between collection size and vocabulary size is linear in log-log space
and the assumption of linearity is usually born out in
practice as shown in Figure 5.1 for Reuters-RCV1.
In this case, the fit is excellent for
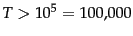 , for the parameter values
, for the parameter values 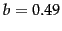 and
and
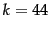 . For example, for the first 1,000,020 tokens Heaps'
law predicts 38,323 terms:
. For example, for the first 1,000,020 tokens Heaps'
law predicts 38,323 terms:
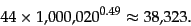 |
(2) |
The actual number is
38,365 terms, very close to the prediction.
The parameter  is quite variable because vocabulary
growth depends a lot on the nature of the collection and how
it is processed. Case-folding and stemming reduce the growth
rate of the vocabulary, whereas including numbers and
spelling errors increase it. Regardless
of the values of the parameters for a particular collection,
Heaps' law suggests that (i) the dictionary size
continues to increase with more documents in the collection,
rather than a maximum vocabulary size being reached, and
(ii) the size of the dictionary is quite large for
large collections. These two hypotheses have been
empirically shown to be true of large text collections
(Section 5.4 ). So dictionary compression
is important for an effective information retrieval system.
is quite variable because vocabulary
growth depends a lot on the nature of the collection and how
it is processed. Case-folding and stemming reduce the growth
rate of the vocabulary, whereas including numbers and
spelling errors increase it. Regardless
of the values of the parameters for a particular collection,
Heaps' law suggests that (i) the dictionary size
continues to increase with more documents in the collection,
rather than a maximum vocabulary size being reached, and
(ii) the size of the dictionary is quite large for
large collections. These two hypotheses have been
empirically shown to be true of large text collections
(Section 5.4 ). So dictionary compression
is important for an effective information retrieval system.





Next: Zipf's law: Modeling the
Up: Statistical properties of terms
Previous: Statistical properties of terms
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![\includegraphics[width=9cm]{art/heapsmall.eps}](img236.png) Heaps' law.Vocabulary size
Heaps' law.Vocabulary size ![\includegraphics[width=9cm]{art/heapsmall.eps}](img236.png) Heaps' law.Vocabulary size
Heaps' law.Vocabulary size ![]() is Heaps'
law , which
estimates vocabulary size as a function of collection size:
is Heaps'
law , which
estimates vocabulary size as a function of collection size:
![]() is quite variable because vocabulary
growth depends a lot on the nature of the collection and how
it is processed. Case-folding and stemming reduce the growth
rate of the vocabulary, whereas including numbers and
spelling errors increase it. Regardless
of the values of the parameters for a particular collection,
Heaps' law suggests that (i) the dictionary size
continues to increase with more documents in the collection,
rather than a maximum vocabulary size being reached, and
(ii) the size of the dictionary is quite large for
large collections. These two hypotheses have been
empirically shown to be true of large text collections
(Section 5.4 ). So dictionary compression
is important for an effective information retrieval system.
is quite variable because vocabulary
growth depends a lot on the nature of the collection and how
it is processed. Case-folding and stemming reduce the growth
rate of the vocabulary, whereas including numbers and
spelling errors increase it. Regardless
of the values of the parameters for a particular collection,
Heaps' law suggests that (i) the dictionary size
continues to increase with more documents in the collection,
rather than a maximum vocabulary size being reached, and
(ii) the size of the dictionary is quite large for
large collections. These two hypotheses have been
empirically shown to be true of large text collections
(Section 5.4 ). So dictionary compression
is important for an effective information retrieval system.