




Next: Dictionary compression
Up: Statistical properties of terms
Previous: Heaps' law: Estimating the
Contents
Index
Zipf's law: Modeling the distribution of terms
We also want to understand
how terms are distributed across documents. This
helps us to characterize the properties of the
algorithms for compressing postings lists in Section 5.3 .
A commonly used model of the distribution of terms in a
collection is Zipf's law . It states that, if
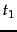 is the
most common term in the collection,
is the
most common term in the collection, 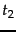 is the next most
common, and so on, then the collection frequency
is the next most
common, and so on, then the collection frequency
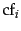 of the
of the 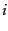 th most common
term is proportional to
th most common
term is proportional to 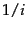 :
:
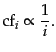 |
|
|
(3) |
So if the most frequent term occurs 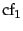 times, then the
second most frequent term has half as many occurrences, the third
most frequent term a third as many occurrences, and so on. The
intuition is that frequency decreases very rapidly with
rank. Equation 3 is one of the simplest ways of
formalizing such a rapid decrease and it has been found to
be a reasonably good model.
times, then the
second most frequent term has half as many occurrences, the third
most frequent term a third as many occurrences, and so on. The
intuition is that frequency decreases very rapidly with
rank. Equation 3 is one of the simplest ways of
formalizing such a rapid decrease and it has been found to
be a reasonably good model.
Equivalently, we can write Zipf's law as
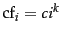 or
as
or
as
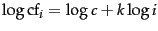 where
where 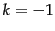 and
and 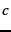 is
a constant to be defined in Section 5.3.2 . It is therefore a
power law with exponent
is
a constant to be defined in Section 5.3.2 . It is therefore a
power law with exponent 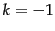 . See
Chapter 19 , page 19.2.1 , for another
power law, a law characterizing the distribution of links on web
pages.
. See
Chapter 19 , page 19.2.1 , for another
power law, a law characterizing the distribution of links on web
pages.
![\includegraphics[width=9cm]{art/zipfnew.eps}](img253.png)
Zipf's law for Reuters-RCV1.
Frequency is plotted as a function of frequency rank for
the terms in the
collection. The line is the distribution predicted by Zipf's
law (weighted least-squares fit; intercept is 6.95).
The log-log graph in Figure 5.2 plots the
collection frequency of a term as a function of its rank for
Reuters-RCV1. A line with slope -1, corresponding to
the Zipf function
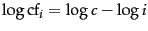 , is also shown.
The fit of the data to the law is not particularly good, but
good enough to serve as a model for term distributions in
our calculations in Section 5.3 .
, is also shown.
The fit of the data to the law is not particularly good, but
good enough to serve as a model for term distributions in
our calculations in Section 5.3 .
Exercises.
- Assuming one machine word per posting, what is the
size of the uncompressed (nonpositional) index for
different tokenizations based on Table 5.1 ? How do these
numbers compare with Table 5.6 ?





Next: Dictionary compression
Up: Statistical properties of terms
Previous: Heaps' law: Estimating the
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() is the
most common term in the collection,
is the
most common term in the collection, ![]() is the next most
common, and so on, then the collection frequency
is the next most
common, and so on, then the collection frequency
![]() of the
of the ![]() th most common
term is proportional to
th most common
term is proportional to ![]() :
:
![]() or
as
or
as
![]() where
where ![]() and
and ![]() is
a constant to be defined in Section 5.3.2 . It is therefore a
power law with exponent
is
a constant to be defined in Section 5.3.2 . It is therefore a
power law with exponent ![]() . See
Chapter 19 , page 19.2.1 , for another
power law, a law characterizing the distribution of links on web
pages.
. See
Chapter 19 , page 19.2.1 , for another
power law, a law characterizing the distribution of links on web
pages.
![\includegraphics[width=9cm]{art/zipfnew.eps}](img253.png) Zipf's law for Reuters-RCV1.
Frequency is plotted as a function of frequency rank for
the terms in the
collection. The line is the distribution predicted by Zipf's
law (weighted least-squares fit; intercept is 6.95).
Zipf's law for Reuters-RCV1.
Frequency is plotted as a function of frequency rank for
the terms in the
collection. The line is the distribution predicted by Zipf's
law (weighted least-squares fit; intercept is 6.95).
![]() , is also shown.
The fit of the data to the law is not particularly good, but
good enough to serve as a model for term distributions in
our calculations in Section 5.3 .
, is also shown.
The fit of the data to the law is not particularly good, but
good enough to serve as a model for term distributions in
our calculations in Section 5.3 .