Learning weights

How do we determine the weights 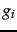$g_i$ for weighted zone scoring? These weights could be specified by an expert (or, in principle, the user); but increasingly, these weights are ``learned'' using training examples that have been judged editorially. This latter methodology falls under a general class of approaches to scoring and ranking in information retrieval, known as machine-learned relevance . We provide a brief introduction to this topic here because weighted zone scoring presents a clean setting for introducing it; a complete development demands an understanding of machine learning and is deferred to Chapter 15 .

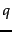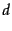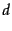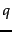1. We are provided with a set of training examples, each of which is a tuple consisting of a query $q$ and a document $d$, together with a relevance judgment for $d$ on $q$. In the simplest form, each relevance judgments is either Relevant or Non-relevant. More sophisticated implementations of the methodology make use of more nuanced judgments.
2. The weights 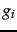$g_i$ are then ``learned'' from these examples, in order that the learned scores approximate the relevance judgments in the training examples.

For weighted zone scoring, the process may be viewed as learning a linear function of the Boolean match scores contributed by the various zones. The expensive component of this methodology is the labor-intensive assembly of user-generated relevance judgments from which to learn the weights, especially in a collection that changes frequently (such as the Web). We now detail a simple example that illustrates how we can reduce the problem of learning the weights 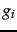$g_i$ to a simple optimization problem.

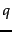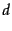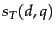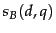We now consider a simple case of weighted zone scoring, where each document has a title zone and a body zone. Given a query $q$ and a document $d$, we use the given Boolean match function to compute Boolean variables $s_T(d,q)$ and $s_B(d,q)$, depending on whether the title (respectively, body) zone of 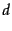$d$ matches query 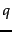$q$. For instance, the algorithm in Figure 6.4 uses an AND of the query terms for this Boolean function. 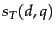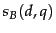We will compute a score between 0 and 1 for each (document, query) pair using $s_T(d,q)$ and $s_B(d,q)$ by using a constant $g\in[0,1]$, as follows:

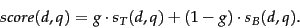$$score(d,q)=g\cdot s_T(d,q) + (1-g)\cdot s_B(d,q).$$ (14)

We now describe how to determine the constant 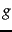$g$ from a set of training examples, each of which is a triple of the form 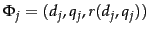$\Phi_j=(d_j, q_j, r(d_j, q_j))$. In each training example, a given training document 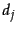$d_j$ and a given training query 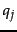$q_j$ are assessed by a human editor who delivers a relevance judgment 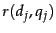$r(d_j, q_j)$ that is either Relevant or Non-relevant. This is illustrated in Figure 6.5 , where seven training examples are shown.

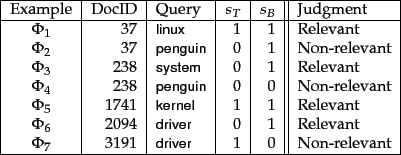
Figure 6.5: An illustration of training examples.

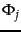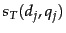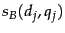For each training example $\Phi_j$ we have Boolean values $s_T(d_j,q_j)$ and $s_B(d_j,q_j)$ that we use to compute a score from (14)

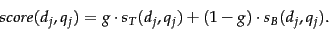$$score(d_j,q_j)=g\cdot s_T(d_j,q_j) + (1-g)\cdot s_B(d_j,q_j).$$ (15)

We now compare this computed score to the human relevance judgment for the same document-query pair 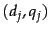$(d_j,q_j)$; to this end, we will quantize each Relevant judgment as a 1 and each Non-relevant judgment as a 0. Suppose that we define the error of the scoring function with weight 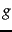$g$ as

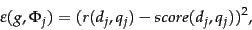$$\varepsilon(g,\Phi_j)=(r(d_j, q_j)-score(d_j,q_j))^2,$$ (16)

where we have quantized the editorial relevance judgment 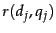$r(d_j, q_j)$ to 0 or 1. Then, the total error of a set of training examples is given by

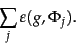$$\sum_{j}\varepsilon(g,\Phi_j).$$ (17)

The problem of learning the constant 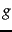$g$ from the given training examples then reduces to picking the value of 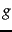$g$ that minimizes the total error in (17).

Picking the best value of 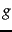$g$ in (17) in the formulation of Section 6.1.3 reduces to the problem of minimizing a quadratic function of 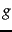$g$ over the interval $[0,1]$. This reduction is detailed in Section 6.1.3 .