




Next: Term frequency and weighting
Up: Parametric and zone indexes
Previous: Learning weights
Contents
Index
The optimal weight g
We begin by noting that for any training example 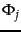 for which
for which
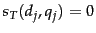 and
and
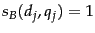 , the score computed by Equation 14 is
, the score computed by Equation 14 is 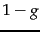 . In similar fashion, we may write down the score computed by Equation 14 for the three other possible combinations of
. In similar fashion, we may write down the score computed by Equation 14 for the three other possible combinations of 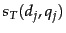 and
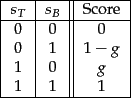
and 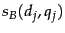 ; this is summarized in Figure 6.6 .
; this is summarized in Figure 6.6 .
Figure 6.6:
The four possible combinations of 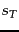 and
and 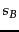 .
.
 |
Let 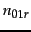 (respectively,
(respectively, 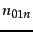 ) denote the number of training examples for which
) denote the number of training examples for which
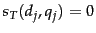 and
and
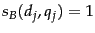 and the editorial judgment is Relevant (respectively, Non-relevant). Then the contribution to the total error in Equation 17 from training examples for which
and the editorial judgment is Relevant (respectively, Non-relevant). Then the contribution to the total error in Equation 17 from training examples for which
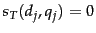 and
and
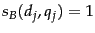 is
is
![\begin{displaymath}[1-(1-g)]^2n_{01r} + [0-(1-g)]^2n_{01n}.
\end{displaymath}](img393.png) |
(18) |
By writing in similar fashion the error contributions from training examples of the other three combinations of values for 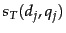 and
and 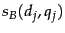 (and extending the notation in the obvious manner), the total error corresponding to Equation 17 is
(and extending the notation in the obvious manner), the total error corresponding to Equation 17 is
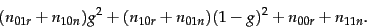 |
(19) |
By differentiating Equation 19 with respect to 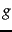 and setting the result to zero, it follows that the optimal value of
and setting the result to zero, it follows that the optimal value of 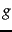 is
is
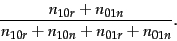 |
(20) |
Exercises.
- When using weighted zone scoring, is it necessary for all zones to use the same Boolean match function?
- In Example 6.1.1 above with weights
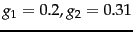 and
and 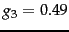 , what are all the distinct score values a document may get?
, what are all the distinct score values a document may get?
- Rewrite the algorithm in Figure 6.4
to the case of more than two query terms.
- Write pseudocode for the function WeightedZone for the case of two postings lists in Figure 6.4 .
- Apply Equation 20 to the sample training set in Figure 6.5 to estimate the best value of
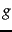 for this sample.
for this sample.
- For the value of
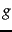 estimated in Exercise 6.1.3, compute the weighted zone score for each (query, document) example. How do these scores relate to the relevance judgments in Figure 6.5 (quantized to 0/1)?
estimated in Exercise 6.1.3, compute the weighted zone score for each (query, document) example. How do these scores relate to the relevance judgments in Figure 6.5 (quantized to 0/1)?
- Why does the expression for
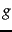 in (20) not involve training examples in which
in (20) not involve training examples in which 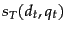 and
and 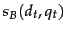 have the same value?
have the same value?





Next: Term frequency and weighting
Up: Parametric and zone indexes
Previous: Learning weights
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() for which
for which
![]() and
and
![]() , the score computed by Equation 14 is
, the score computed by Equation 14 is ![]() . In similar fashion, we may write down the score computed by Equation 14 for the three other possible combinations of
. In similar fashion, we may write down the score computed by Equation 14 for the three other possible combinations of ![]() and
and ![]() ; this is summarized in Figure 6.6 .
; this is summarized in Figure 6.6 .
![]() (respectively,
(respectively, ![]() ) denote the number of training examples for which
) denote the number of training examples for which
![]() and
and
![]() and the editorial judgment is Relevant (respectively, Non-relevant). Then the contribution to the total error in Equation 17 from training examples for which
and the editorial judgment is Relevant (respectively, Non-relevant). Then the contribution to the total error in Equation 17 from training examples for which
![]() and
and
![]() is
is
![]() and setting the result to zero, it follows that the optimal value of
and setting the result to zero, it follows that the optimal value of ![]() is
is