The rank of a matrix is the number of linearly independent rows (or columns) in it; thus,
![]() . A square
. A square ![]() matrix all of whose off-diagonal entries are zero is called a diagonal matrix; its rank is equal to the number of non-zero diagonal entries. If all
matrix all of whose off-diagonal entries are zero is called a diagonal matrix; its rank is equal to the number of non-zero diagonal entries. If all ![]() diagonal entries of such a diagonal matrix are
diagonal entries of such a diagonal matrix are ![]() , it is called the identity matrix of dimension
, it is called the identity matrix of dimension ![]() and represented by
and represented by ![]() .
.
For a square
![]() matrix
matrix ![]() and a vector
and a vector ![]() that is not all zeros, the values of
that is not all zeros, the values of ![]() satisfying
satisfying
The eigenvalues of a matrix are found by solving the
characteristic equation, which is obtained by
rewriting Equation 213 in the form
![]() . The eigenvalues of
. The eigenvalues of ![]() are then the solutions of
are then the solutions of
![]() , where
, where ![]() denotes the determinant of a square matrix
denotes the determinant of a square matrix ![]() .
The equation
.
The equation
![]() is an
is an ![]() th order polynomial equation in
th order polynomial equation in ![]() and can have at most
and can have at most ![]() roots, which are the
eigenvalues of
roots, which are the
eigenvalues of ![]() . These eigenvalues can in general be complex, even if all entries of
. These eigenvalues can in general be complex, even if all entries of ![]() are real.
are real.
We now examine some further properties of eigenvalues and eigenvectors, to set up the central idea of singular value decompositions in Section 18.2 below. First, we look at the relationship between matrix-vector multiplication and eigenvalues.
Worked example.
Consider the matrix
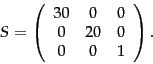 |
(215) |
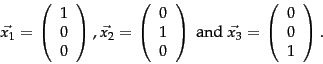 |
(216) |
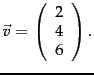 We can always express
We can always express 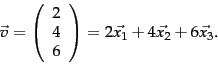 |
(217) |
Example 18.1 shows that even though ![]() is an arbitrary vector, the effect of multiplication by
is an arbitrary vector, the effect of multiplication by ![]() is determined by the eigenvalues and eigenvectors of
is determined by the eigenvalues and eigenvectors of ![]() . Furthermore, it is intuitively apparent from Equation 221 that the product
. Furthermore, it is intuitively apparent from Equation 221 that the product ![]() is relatively unaffected by terms arising from the small eigenvalues of
is relatively unaffected by terms arising from the small eigenvalues of ![]() ; in our example, since
; in our example, since ![]() , the contribution of the third term on the right hand side of Equation 221 is small. In fact, if we were to completely ignore the contribution in Equation 221 from the third eigenvector corresponding to
, the contribution of the third term on the right hand side of Equation 221 is small. In fact, if we were to completely ignore the contribution in Equation 221 from the third eigenvector corresponding to ![]() , then the product
, then the product ![]() would be computed to be
would be computed to be
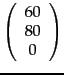 rather than the correct product which is
rather than the correct product which is
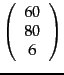 ; these two vectors are relatively close to each other by any of various metrics one could apply (such as the length of their vector difference).
; these two vectors are relatively close to each other by any of various metrics one could apply (such as the length of their vector difference).
This suggests that the effect of small eigenvalues (and their eigenvectors) on a matrix-vector product is small. We will carry forward this intuition when studying matrix decompositions and low-rank approximations in Section 18.2 . Before doing so, we examine the eigenvectors and eigenvalues of special forms of matrices that will be of particular interest to us.
For a symmetric matrix ![]() , the eigenvectors corresponding to distinct eigenvalues are orthogonal. Further, if
, the eigenvectors corresponding to distinct eigenvalues are orthogonal. Further, if ![]() is both real and symmetric, the eigenvalues are all real.
is both real and symmetric, the eigenvalues are all real.
Worked example.
Consider the real, symmetric matrix
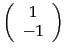 and
and
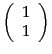 are orthogonal.
End worked example.
are orthogonal.
End worked example.