PageRank

We now focus on scoring and ranking measures derived from the link structure alone. Our first technique for link analysis assigns to every node in the web graph a numerical score between 0 and 1, known as its PageRank . The PageRank of a node will depend on the link structure of the web graph. Given a query, a web search engine computes a composite score for each web page that combines hundreds of features such as cosine similarity (Section 6.3 ) and term proximity (Section 7.2.2 ), together with the PageRank score. This composite score, developed using the methods of Section 15.4.1 , is used to provide a ranked list of results for the query.

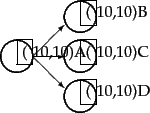
Consider a random surfer who begins at a web page (a node of the web graph) and executes a random walk on the Web as follows. At each time step, the surfer proceeds from his current page A to a randomly chosen web page that A hyperlinks to. Figure 21.1 shows the surfer at a node A, out of which there are three hyperlinks to nodes B, C and D; the surfer proceeds at the next time step to one of these three nodes, with equal probabilities 1/3.

Figure 21.1: The random surfer at node A proceeds with probability 1/3 to each of B, C and D.

As the surfer proceeds in this random walk from node to node, he visits some nodes more often than others; intuitively, these are nodes with many links coming in from other frequently visited nodes. The idea behind PageRank is that pages visited more often in this walk are more important.

What if the current location of the surfer, the node A, has no out-links? To address this we introduce an additional operation for our random surfer: the teleport operation. In the teleport operation the surfer jumps from a node to any other node in the web graph. This could happen because he types an address into the URL bar of his browser. The destination of a teleport operation is modeled as being chosen uniformly at random from all web pages. In other words, if $N$ is the total number of nodes in the web graph, the teleport operation takes the surfer to each node with probability $1/N$. The surfer would also teleport to his present position with probability $1/N$.

In assigning a PageRank score to each node of the web graph, we use the teleport operation in two ways: (1) When at a node with no out-links, the surfer invokes the teleport operation. (2) At any node that has outgoing links, the surfer invokes the teleport operation with probability $0<\alpha<1$ and the standard random walk (follow an out-link chosen uniformly at random as in Figure 21.1 ) with probability $1-\alpha$, where $\alpha$ is a fixed parameter chosen in advance. Typically, $\alpha$ might be 0.1.

In Section 21.2.1 , we will use the theory of Markov chains to argue that when the surfer follows this combined process (random walk plus teleport) he visits each node $v$ of the web graph a fixed fraction of the time $\pi (v)$ that depends on (1) the structure of the web graph and (2) the value of $\alpha$. We call this value $\pi (v)$ the PageRank of $v$ and will show how to compute this value in Section 21.2.2 .