- ...
email.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- In modern parlance, the word ``search'' has tended to replace
``(information) retrieval''; the term ``search'' is quite ambiguous,
but in context we use the two synonymously.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... it.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Formally, we take the transpose of the
matrix to be able to get the terms as column vectors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... retrieval.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Some information
retrieval researchers prefer the term inverted
file, but expressions like
index construction and index compression
are much more common than inverted file construction
and inverted file compression. For consistency, we
use (inverted) index throughout this book.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- In a (non-positional) inverted index, a posting is just a document ID, but it is inherently associated with a term, via the postings list it is placed on; sometimes we will also talk of a (term, docID) pair as a posting.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... merged.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Unix users can note that these steps are similar to use of
the sort and then uniq commands.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... collection.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- The notation
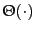 is used to express an asymptotically
tight bound on the complexity of an algorithm. Informally, this is
often written as
is used to express an asymptotically
tight bound on the complexity of an algorithm. Informally, this is
often written as 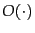 , but this notation really expresses an
asymptotic upper bound, which need not be tight
(Cormen et al., 1990).
, but this notation really expresses an
asymptotic upper bound, which need not be tight
(Cormen et al., 1990).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ,
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- A classifier is a function that takes objects of some sort
and assigns them to one of a number of distinct classes (see Chapter 13 ). Usually
classification is done by machine learning methods such as probabilistic models,
but it can also be done by hand-written rules.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- That is, as defined here, tokens that are
not indexed (stop words) are not terms, and if multiple
tokens are collapsed together via normalization, they are
indexed as one term, under the normalized form.
However, we later relax this definition when discussing classification and
clustering in nbayeslsi, where there is no index. In these
chapters, we drop the requirement of inclusion in the dictionary.
A term means a normalized word.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... query.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- For the free text case, this is straightforward. The Boolean case is
more complex: this tokenization may produce multiple terms from one
query word. This can be handled by combining the terms with an AND
or as a phrase query phrasequery.
It is harder for a system to handle the opposite case where the user
entered as two terms something that was tokenized together in
the document processing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tokens.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- It is also often referred to as term normalization ,
but we prefer to reserve the name term for the output of the
normalization process.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
documents.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- At the time we wrote this chapter (Aug. 2005), this was actually
the case on
Google: the top result for the query C.A.T. was a site
about cats, the Cat Fanciers Web Site http://www.fanciers.com/.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... part-of-speech-tagging.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Part of speech taggers classify words as nouns, verbs, etc. - or,
in practice, often as finer-grained classes like ``plural proper
noun''. Many fairly accurate (c. 96% per-tag accuracy) part-of-speech
taggers now exist,
usually trained by machine learning methods on hand-tagged text.
See, for instance, Manning and Schütze (1999, ch. 10).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... maintain.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- So-called perfect hash functions are designed to preclude collisions, but are rather more complicated both to implement and to compute.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...clusters
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- A cluster
in this chapter is
a group of tightly coupled computers that work together
closely. This sense of the word is different from the use of
cluster as a group of
documents that are semantically similar in flatclustlsi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... structure
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- See,
for example, (Cormen et al., 1990, Chapter 19).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... list.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Note that the origin
is 0 in the table. Because we never need to encode a docID or
a gap of 0, in practice the origin is usually 1, so that
10000000 encodes 1, 10000101 encodes 6 (not 5 as in the
table), and so on.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
removed.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- We assume here that
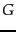 has no leading
0s. If there are any, they are
removed before deleting the leading 1.
has no leading
0s. If there are any, they are
removed before deleting the leading 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
distribution
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Readers who want to review basic
concepts of probability theory
may want to consult
Rice (2006) or
Ross (2006). Note that we are interested in
probability distributions over integers (gaps, frequencies,
etc.), but that the coding properties of a probability
distribution are independent of whether the outcomes are
integers or something else.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Note that, unfortunately, the conventional symbol for both
entropy and harmonic number is
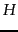 . Context should make
clear which is meant in this chapter.
. Context should make
clear which is meant in this chapter.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... all,
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- A system may not fully order all documents in the collection in
response to a query or at any rate an evaluation exercise may be
based on submitting only the top
 results for each information need.
results for each information need.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... agreement.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- For a contingency table, as in Table 8.2 , a marginal statistic
is formed by summing a
row or column. The marginal
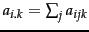 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... need.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- There are exceptions, in domains where recall is
emphasized. For instance, in many legal disclosure cases, a legal associate
will review every document that matches a keyword search.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... find:
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
-
In the equation,
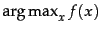 returns a value of
returns a value of 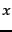 which
maximizes the value of the function
which
maximizes the value of the function 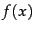 .
Similarly,
.
Similarly,
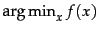 returns a value of
returns a value of 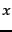 which
minimizes the value of the function
which
minimizes the value of the function 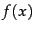 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- In most modern database
systems, one can enable full-text search for text columns.
This usually means that an inverted index is created and
Boolean or vector space search enabled, effectively
combining core database with information retrieval
technologies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- The
representation is simplified in a number of respects. For
example, we
do not show the root node and text is not
embedded in text nodes. See http://www.w3.org/DOM/.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... war.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- To represent the semantics
of NEXI queries fully we would also need to designate one node
in the tree as a ``target node'', for example, the
section in the tree in Figure 10.3 . Without the
designation of a target node, the tree in Figure 10.3 is not
a search for sections embedded in articles (as specified
by NEXI), but a search for articles that contain sections.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... hold.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- The term likelihood is just a synonym of
probability. It is the probability of an event or data
according to a model. The term is usually used when people
are thinking of holding the data fixed, while varying the model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
automaton.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Finite automata can have outputs attached to either their
states or their arcs; we use states here, because that maps
directly on to the way probabilistic automata are usually formalized.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... documents.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- In the IR context that we are leading up to, taking the
stop probability to be fixed across models seems reasonable.
This is because we
are generating queries, and the length distribution of queries is
fixed and independent of the document from which we are generating
the language model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... collection.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
-
Of course, in other cases, they do not. The answer to this within the
language modeling approach is translation language models, as briefly discussed in Section 12.4 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- In the context of probability theory, (re)normalization
refers to summing numbers that cover an event space and dividing
them through by their sum, so that the result is a probability
distribution which sums to 1. This is distinct from both the
concept of term normalization in Chapter 2 and
the concept of length normalization in Chapter 6 , which is
done with a
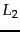 norm.
norm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... model.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- It is also referred to as Jelinek-Mercer smoothing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- We will explain in the next section
why
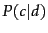 is proportional to (
is proportional to (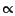 ), not equal to the quantity on
the right.
), not equal to the quantity on
the right.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Our assumption here
is that the length of test documents is bounded.
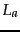 would exceed
would exceed 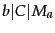 for extremely long
test documents.
for extremely long
test documents.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
magnitude.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- In fact, if the length of documents is not
bounded, the number of parameters in the multinomial case
is infinite.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... symbol.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Our terminology is
nonstandard. The random variable
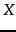 is a
categorical variable, not a multinomial variable, and the
corresponding NB model should perhaps be called a
sequence model . We have chosen to present this sequence model and the multinomial model in Section 13.4.1 as the same
model because they are computationally identical.
is a
categorical variable, not a multinomial variable, and the
corresponding NB model should perhaps be called a
sequence model . We have chosen to present this sequence model and the multinomial model in Section 13.4.1 as the same
model because they are computationally identical.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Take care not to confuse expected mutual
information with pointwise mutual information, which is
defined as
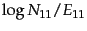 where
where
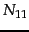 and
and 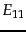 are defined as in
Equation 133.
The two
measures have different properties. See
Section 13.7 .
are defined as in
Equation 133.
The two
measures have different properties. See
Section 13.7 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Feature scores were computed on the first
100,000 documents, except for poultry, a rare class, for
which 800,000 documents were used. We have omitted
numbers and other special words from the top
ten lists.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Reuters-RCV1.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- We trained the classifiers on the first
100,000 documents and computed
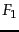 on the next
100,000. The graphs are averages over five classes.
on the next
100,000. The graphs are averages over five classes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wrong.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- We can make this
inference because,
if the two events are
independent, then
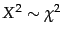 , where
, where 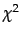 is the
is the
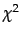 distribution. See, for example,
Rice (2006).
distribution. See, for example,
Rice (2006).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vector
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Recall from basic linear algebra that
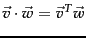 , i.e., the
dot product of
, i.e., the
dot product of 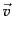 and
and 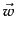 equals the product
by matrix multiplication of the transpose of
equals the product
by matrix multiplication of the transpose of 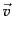 and
and
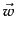 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
classification.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- We
write
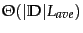 for
for 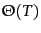 and assume
that the length of
test
documents is bounded as we did on
page 13.2 .
and assume
that the length of
test
documents is bounded as we did on
page 13.2 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ).
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
-
The generalization of a polygon to higher dimensions is a
polytope . A polytope is a region in
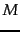 -dimensional space
bounded by
-dimensional space
bounded by 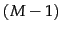 -dimensional hyperplanes.
In
-dimensional hyperplanes.
In 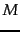 dimensions, the decision boundaries for kNN
consist of segments of
dimensions, the decision boundaries for kNN
consist of segments of
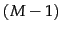 -dimensional hyperplanes that form
the Voronoi tessellation into convex polytopes for the training set
of documents. The decision criterion of assigning a document
to the majority class of its
-dimensional hyperplanes that form
the Voronoi tessellation into convex polytopes for the training set
of documents. The decision criterion of assigning a document
to the majority class of its  nearest neighbors
applies equally to
nearest neighbors
applies equally to 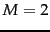 (tessellation into polygons) and
(tessellation into polygons) and 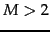 (tessellation into polytopes).
(tessellation into polytopes).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...polytomous
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- A synonym
of polytomous is polychotomous.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... it.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- As discussed in Section 14.1 (page
![[*]](http://nlp.stanford.edu/IR-book/html/icons/crossref.png) ), we present the general case of points
in a vector space, but if the points are length normalized document vectors,
then all the action is taking place on the surface of a unit sphere,
and the decision surface intersects the sphere's surface.
), we present the general case of points
in a vector space, but if the points are length normalized document vectors,
then all the action is taking place on the surface of a unit sphere,
and the decision surface intersects the sphere's surface.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gives:
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Recall that
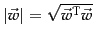 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- We
write
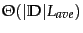 for
for 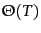 (page 13.2 ) and assume
that the length of
test
documents is bounded as we did on
page 13.2 .
(page 13.2 ) and assume
that the length of
test
documents is bounded as we did on
page 13.2 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
SVM\@.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Materializing the features refers to directly calculating higher
order and interaction terms and then putting them into a linear model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- These results are in terms of the break-even
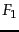 (see Section 8.4 ). Many researchers disprefer
this measure for text classification evaluation, since its
calculation may involve interpolation rather than an actual
parameter setting of the system and it is not clear why this value
should be reported rather than maximal
(see Section 8.4 ). Many researchers disprefer
this measure for text classification evaluation, since its
calculation may involve interpolation rather than an actual
parameter setting of the system and it is not clear why this value
should be reported rather than maximal 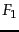 or another point on
the precision/recall curve motivated by the task at hand.
While earlier results in (Joachims, 1998) suggested notable gains
on this task from the use
of higher order polynomial or rbf kernels, this was with
hard-margin SVMs. With soft-margin SVMs, a simple linear SVM with
the default
or another point on
the precision/recall curve motivated by the task at hand.
While earlier results in (Joachims, 1998) suggested notable gains
on this task from the use
of higher order polynomial or rbf kernels, this was with
hard-margin SVMs. With soft-margin SVMs, a simple linear SVM with
the default 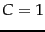 performs best.
performs best.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... modest.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Using the small hierarchy in Figure 13.1 (page
![[*]](http://nlp.stanford.edu/IR-book/html/icons/crossref.png) ) as an
example, the leaf classes are ones like poultry and
coffee, as opposed to higher-up classes like industries.
) as an
example, the leaf classes are ones like poultry and
coffee, as opposed to higher-up classes like industries.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
feasible.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- An upper bound on the number of
clusterings is
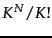 . The
exact number of different partitions of
. The
exact number of different partitions of 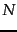 documents into
documents into
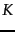 clusters is the Stirling number of the second kind. See
http://mathworld.wolfram.com/StirlingNumberoftheSecondKind.html
or Comtet (1974).
clusters is the Stirling number of the second kind. See
http://mathworld.wolfram.com/StirlingNumberoftheSecondKind.html
or Comtet (1974).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Recall our note of caution from
Figure 14.2 (page 14.2 ) when looking at
this and other 2D figures in this and the following
chapter: these illustrations
can be misleading because 2D projections of length-normalized
vectors distort
similarities and distances between points.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
model.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
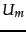 is the random variable we
defined in Section 13.3 (page 13.4 ) for the
Bernoulli Naive Bayes model. It takes the values 1 (term
is the random variable we
defined in Section 13.3 (page 13.4 ) for the
Bernoulli Naive Bayes model. It takes the values 1 (term
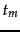 is present in the document) and 0 (term
is present in the document) and 0 (term
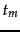 is absent in the document).
is absent in the document).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... EM.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- For example, this problem is common when EM is used to
estimate parameters of
hidden Markov models, probabilistic grammars, and machine
translation models
in natural
language processing
(Manning and Schütze, 1999).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
clustering.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- In this chapter, we only consider
hierarchies
that are
binary
trees like the one shown in Figure 17.1 - but hierarchical
clustering can be easily extended to other types of trees.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... updated.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- We assume
that we use a deterministic method for breaking ties,
such as always choose the merge that is the first cluster with respect to a
total ordering of the subsets of the document set
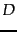 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (a))
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Throughout this chapter, we equate
similarity with proximity in 2D depictions of clustering.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
similarity.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- If you are bothered by the possibility
of ties, assume that
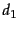 has coordinates
has coordinates
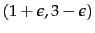 and that all other points have
integer coordinates.
and that all other points have
integer coordinates.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
labeling.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Selecting the most frequent terms is
a non-differential
feature selection technique we discussed in Section 13.5 .
It can also be used for labeling clusters.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 2.1.
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Cf. Zipf's law of the distribution of words in text in Chapter 5 (page 5.2 ), which is a power law with
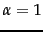 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... host
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- The number of hosts is assumed to far exceed
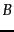 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cluster
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Please note the different usage of ``clusters'' elsewhere in this book, in the sense of Chapters 16 17 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... graph
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- This is consistent with our usage of
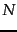 for the number of documents in the collection.
for the number of documents in the collection.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
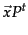
![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
- Note that
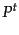 represents
represents 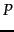 raised to the
raised to the 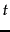 th power, not the transpose of
th power, not the transpose of 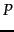 which is denoted
which is denoted 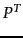 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.