




Next: The Probability Ranking Principle
Up: Probabilistic information retrieval
Previous: Probabilistic information retrieval
Contents
Index
Review of basic probability theory
We hope that the reader has seen a little basic probability
theory previously. We will give a very quick review; some
references for further reading appear at the end of the
chapter. A variable 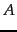 represents an event (a subset of the
space of possible outcomes). Equivalently, we can represent
the subset via a random
variable , which is a function from
outcomes to real numbers; the subset is the domain over which
the random variable
represents an event (a subset of the
space of possible outcomes). Equivalently, we can represent
the subset via a random
variable , which is a function from
outcomes to real numbers; the subset is the domain over which
the random variable 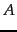 has a particular
value.
Often we
will not know with certainty whether an event is true in the
world. We can ask the probability of the event
has a particular
value.
Often we
will not know with certainty whether an event is true in the
world. We can ask the probability of the event
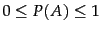 . For two events
. For two events 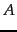 and
and 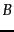 , the
joint event of both events occurring is described by the joint probability
, the
joint event of both events occurring is described by the joint probability
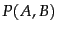 . The conditional probability
. The conditional probability 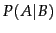 expresses
the probability of event
expresses
the probability of event 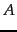 given that event
given that event 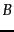 occurred.
The fundamental relationship between joint and
conditional probabilities is given by the chain
rule :
occurred.
The fundamental relationship between joint and
conditional probabilities is given by the chain
rule :
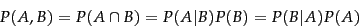 |
(56) |
Without making any assumptions, the probability of a joint event equals the probability of one of the events multiplied by the probability of the other event conditioned on knowing the first event happened.
Writing
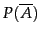 for the complement of an event, we similarly have:
for the complement of an event, we similarly have:
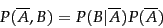 |
(57) |
Probability theory also has a partition rule , which says that if an event 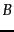 can be divided into an exhaustive set of disjoint subcases, then the probability of
can be divided into an exhaustive set of disjoint subcases, then the probability of 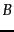 is the sum of the probabilities of the subcases. A special case of this rule gives that:
is the sum of the probabilities of the subcases. A special case of this rule gives that:
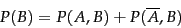 |
(58) |
From these we can derive Bayes' Rule for inverting conditional probabilities:
![\begin{displaymath}P(A\vert B) = \frac{P(B\vert A)P(A)}{P(B)} = \left[\frac{P(...
...{\sum_{X \in \{ A, \overline{A}\}} P(B\vert X)P(X)}\right]P(A)
\end{displaymath}](img682.png) |
(59) |
This equation can also be thought of as a way of updating probabilities. We start off with an initial estimate of how likely the event 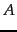 is when we do not have any other information; this is the prior probability
is when we do not have any other information; this is the prior probability 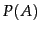 . Bayes' rule lets us derive a posterior probability
. Bayes' rule lets us derive a posterior probability 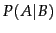 after having seen the evidence
after having seen the evidence 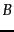 , based on the likelihood of
, based on the likelihood of 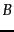 occurring in the two cases that
occurring in the two cases that 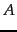 does or does not hold.
does or does not hold.![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
Finally, it is often useful to talk about the odds of an event, which provide a kind of multiplier for how probabilities change:
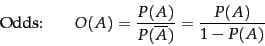 |
(60) |





Next: The Probability Ranking Principle
Up: Probabilistic information retrieval
Previous: Probabilistic information retrieval
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() represents an event (a subset of the
space of possible outcomes). Equivalently, we can represent
the subset via a random
variable , which is a function from
outcomes to real numbers; the subset is the domain over which
the random variable
represents an event (a subset of the
space of possible outcomes). Equivalently, we can represent
the subset via a random
variable , which is a function from
outcomes to real numbers; the subset is the domain over which
the random variable ![]() has a particular
value.
Often we
will not know with certainty whether an event is true in the
world. We can ask the probability of the event
has a particular
value.
Often we
will not know with certainty whether an event is true in the
world. We can ask the probability of the event
![]() . For two events
. For two events ![]() and
and ![]() , the
joint event of both events occurring is described by the joint probability
, the
joint event of both events occurring is described by the joint probability
![]() . The conditional probability
. The conditional probability ![]() expresses
the probability of event
expresses
the probability of event ![]() given that event
given that event ![]() occurred.
The fundamental relationship between joint and
conditional probabilities is given by the chain
rule :
occurred.
The fundamental relationship between joint and
conditional probabilities is given by the chain
rule :
![]() for the complement of an event, we similarly have:
for the complement of an event, we similarly have: