Single-pass in-memory indexing

Blocked sort-based indexing has excellent scaling properties, but it needs a data structure for mapping terms to termIDs. For very large collections, this data structure does not fit into memory. A more scalable alternative is single-pass in-memory indexing or SPIMI . SPIMI uses terms instead of termIDs, writes each block's dictionary to disk, and then starts a new dictionary for the next block. SPIMI can index collections of any size as long as there is enough disk space available.

Figure 4.4: Inversion of a block in single-pass in-memory indexing

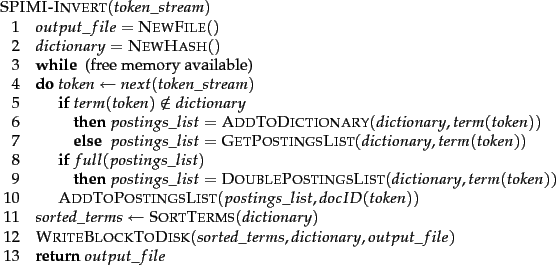
The SPIMI algorithm is shown in Figure 4.4 . The part of the algorithm that parses documents and turns them into a stream of term-docID pairs, which we call tokens here, has been omitted. SPIMI-INVERT is called repeatedly on the token stream until the entire collection has been processed.

Tokens are processed one by one (line 4)

during each successive call of SPIMI-INVERT. When a term occurs for the first time, it is added to the dictionary (best implemented as a hash), and a new postings list is created (line 6). The call in line 7 returns this postings list for subsequent occurrences of the term.

A difference between BSBI and SPIMI is that SPIMI adds a posting directly to its postings list (line 10). Instead of first collecting all termID-docID pairs and then sorting them (as we did in BSBI), each postings list is dynamic (i.e., its size is adjusted as it grows) and it is immediately available to collect postings. This has two advantages: It is faster because there is no sorting required, and it saves memory because we keep track of the term a postings list belongs to, so the termIDs of postings need not be stored. As a result, the blocks that individual calls of SPIMI-INVERT can process are much larger and the index construction process as a whole is more efficient.

Because we do not know how large the postings list of a term will be when we first encounter it, we allocate space for a short postings list initially and double the space each time it is full (lines 8-9). This means that some memory is wasted, which counteracts the memory savings from the omission of termIDs in intermediate data structures. However, the overall memory requirements for the dynamically constructed index of a block in SPIMI are still lower than in BSBI.

When memory has been exhausted, we write the index of the block (which consists of the dictionary and the postings lists) to disk (line 12). We have to sort the terms (line 11) before doing this because we want to write postings lists in lexicographic order to facilitate the final merging step. If each block's postings lists were written in unsorted order, merging blocks could not be accomplished by a simple linear scan through each block.

Each call of SPIMI-INVERT writes a block to disk, just as in BSBI. The last step of SPIMI (corresponding to line 7 in Figure 4.2 ; not shown in Figure 4.4 ) is then to merge the blocks into the final inverted index.

In addition to constructing a new dictionary structure for each block and eliminating the expensive sorting step, SPIMI has a third important component: compression. Both the postings and the dictionary terms can be stored compactly on disk if we employ compression. Compression increases the efficiency of the algorithm further because we can process even larger blocks, and because the individual blocks require less space on disk. We refer readers to the literature for this aspect of the algorithm (Section 4.7 ).

The time complexity of SPIMI is $\Theta(T)$ because no sorting of tokens is required and all operations are at most linear in the size of the collection.