




Next: Feature selection
Up: Properties of Naive Bayes
Previous: Properties of Naive Bayes
Contents
Index
A variant of the multinomial model
An alternative formalization of the
represents each document 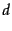 as an
as an 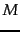 -dimensional vector of counts
-dimensional vector of counts
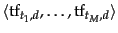 where
where
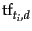 is the term frequency of
is the term frequency of 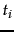 in
in 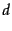 .
.
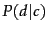 is then computed as follows
(cf. Equation 99, page 12.2.1 );
is then computed as follows
(cf. Equation 99, page 12.2.1 );
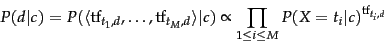 |
(129) |
Note that we have omitted the
multinomial factor. See Equation 99 (page 99 ).
Equation 129 is equivalent to the sequence model in
Equation 113 as
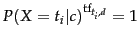 for terms that do not occur in
for terms that do not occur in 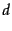 (
(
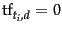 ) and
a term that occurs
) and
a term that occurs
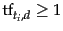 times will contribute
times will contribute
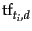 factors both in Equation 113
and in Equation 129.
factors both in Equation 113
and in Equation 129.
Exercises.
- Which of the documents in
Table 13.5 have identical and different bag of
words representations for (i) the Bernoulli model (ii) the
multinomial model? If there are differences, describe them.
- The rationale for the positional independence
assumption is that there is no useful information in the
fact that a term occurs in position
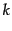 of a document. Find
exceptions. Consider formulaic documents with a fixed
document structure.
of a document. Find
exceptions. Consider formulaic documents with a fixed
document structure.
- Table 13.3 gives Bernoulli and
multinomial estimates for the word the. Explain the
difference.





Next: Feature selection
Up: Properties of Naive Bayes
Previous: Properties of Naive Bayes
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() for terms that do not occur in
for terms that do not occur in ![]() (
(
![]() ) and
a term that occurs
) and
a term that occurs
![]() times will contribute
times will contribute
![]() factors both in Equation 113
and in Equation 129.
factors both in Equation 113
and in Equation 129.