




Next: Mutual information
Up: Text classification and Naive
Previous: A variant of the
Contents
Index
Feature selection
Feature selection
is the process of selecting a subset of the terms
occurring in
the training set and using only this subset as features
in text classification. Feature selection
serves two main purposes. First, it makes training and
applying a classifier more efficient by decreasing the size
of the effective vocabulary. This is of particular
importance for classifiers that, unlike NB, are
expensive to train. Second, feature selection often
increases classification accuracy by eliminating noise
features. A noise feature
is one that, when added to the document representation,
increases the classification error on new data. Suppose a
rare term, say arachnocentric, has no information
about a class, say China, but all instances of
arachnocentric happen to occur in
China documents in our training set. Then the learning method might
produce a classifier that misassigns test documents containing
arachnocentric to China. Such an incorrect
generalization from an accidental property of the training
set is called overfitting .
Figure:
Basic feature selection algorithm for selecting the
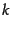 best features.
best features.
 |
We can view feature selection as a method for replacing a
complex classifier (using all features) with a
simpler one (using a subset of the
features). It may appear counterintuitive at first that a
seemingly weaker classifier is advantageous in statistical text
classification,
but when discussing
the bias-variance tradeoff in
Section 14.6 (page ![[*]](http://nlp.stanford.edu/IR-book/html/icons/crossref.png) ), we will see
that weaker models are often preferable when limited
training data are available.
), we will see
that weaker models are often preferable when limited
training data are available.
The basic feature selection algorithm is shown in
Figure 13.6 .
For a given class 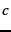 ,
we compute a utility measure
,
we compute a utility measure 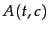 for each
term of the vocabulary and select the
for each
term of the vocabulary and select the 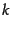 terms that have the highest values of
terms that have the highest values of 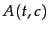 . All
other terms are discarded and not used in classification. We will
introduce three different utility measures in this section: mutual information,
. All
other terms are discarded and not used in classification. We will
introduce three different utility measures in this section: mutual information,
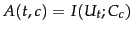 ; the
; the 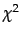 test,
test,
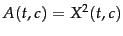 ; and frequency,
; and frequency,
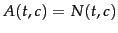 .
.
Of the two NB models, the Bernoulli model is particularly
sensitive to noise features. A Bernoulli NB classifier
requires some form of feature selection or else its accuracy will
be low.
This section mainly addresses feature selection for two-class
classification tasks like
China versus
not-China. Section 13.5.5 briefly discusses
optimizations for systems with more than two
classes.
Subsections





Next: Mutual information
Up: Text classification and Naive
Previous: A variant of the
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07

![]() ), we will see
that weaker models are often preferable when limited
training data are available.
), we will see
that weaker models are often preferable when limited
training data are available.
![]() ,
we compute a utility measure
,
we compute a utility measure ![]() for each
term of the vocabulary and select the
for each
term of the vocabulary and select the ![]() terms that have the highest values of
terms that have the highest values of ![]() . All
other terms are discarded and not used in classification. We will
introduce three different utility measures in this section: mutual information,
. All
other terms are discarded and not used in classification. We will
introduce three different utility measures in this section: mutual information,
![]() ; the
; the ![]() test,
test,
![]() ; and frequency,
; and frequency,
![]() .
.