




Next: Hierarchical clustering
Up: Flat clustering
Previous: References and further reading
Contents
Index
Exercises.
- Let
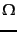 be a clustering
that exactly reproduces a class structure
be a clustering
that exactly reproduces a class structure 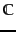 and
and 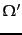 a clustering that further subdivides some clusters in
a clustering that further subdivides some clusters in 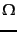 . Show
that
. Show
that
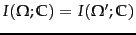 .
.
- Show that
![$I(\Omega; \mathbb{C}) \leq [H(\Omega)+
H(\mathbb{C} )]/2$](img1539.png) .
.
- Mutual information is symmetric in the sense that
its value
does not change if the roles of clusters and
classes are switched:
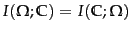 .
Which of the other three evaluation measures are symmetric
in this sense?
.
Which of the other three evaluation measures are symmetric
in this sense?
- Compute RSS for the two clusterings in Figure 16.7 .
- (i) Give an example of a
set of points and three initial centroids (which need not be
members of the set of points) for which 3-means
converges to a clustering with an empty cluster. (ii) Can
a clustering with an empty cluster be the global
optimum with respect to RSS?
- Download
Reuters-21578.
Discard documents that do not occur in one of the 10 classes
acquisitions,
corn,
crude,
earn,
grain,
interest,
money-fx,
ship,
trade, and
wheat. Discard documents that occur in two of these
10 classes.
(i) Compute a
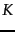 -means clustering of this subset
into 10 clusters.
There are a number of software packages that implement
-means clustering of this subset
into 10 clusters.
There are a number of software packages that implement
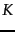 -means, such as WEKA (Witten and Frank, 2005) and R
(R Development Core Team, 2005).
(ii) Compute purity, normalized mutual
information,
-means, such as WEKA (Witten and Frank, 2005) and R
(R Development Core Team, 2005).
(ii) Compute purity, normalized mutual
information, 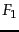 and RI for the clustering with respect to
the 10 classes.
(iii)
Compile a confusion matrix
(Table 14.5 , page 14.5 ) for the 10
classes and 10 clusters.
Identify classes that give rise to false
positives
and false negatives.
and RI for the clustering with respect to
the 10 classes.
(iii)
Compile a confusion matrix
(Table 14.5 , page 14.5 ) for the 10
classes and 10 clusters.
Identify classes that give rise to false
positives
and false negatives.
- Prove that
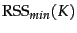 is monotonically decreasing in
is monotonically decreasing in 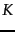 .
.
- There is a soft version of
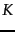 -means
that computes the fractional membership of a document in a
cluster as a monotonically decreasing function of the
distance
-means
that computes the fractional membership of a document in a
cluster as a monotonically decreasing function of the
distance 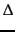 from its centroid, e.g., as
from its centroid, e.g., as 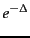 .
Modify reassignment and
recomputation steps of hard
.
Modify reassignment and
recomputation steps of hard 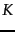 -means for this soft version.
-means for this soft version.
- In the last iteration in Table 16.3 , document 6 is in cluster 2 even
though it was the initial seed for cluster 1. Why does the
document change membership?
- The values of the parameters
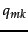 in iteration
25 in Table 16.3 are rounded. What are the exact values
that EM will converge to?
in iteration
25 in Table 16.3 are rounded. What are the exact values
that EM will converge to?
- Perform a
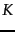 -means clustering for the documents in
Table 16.3 .
After how many iterations does
-means clustering for the documents in
Table 16.3 .
After how many iterations does 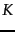 -means converge?
Compare the result with the EM clustering
in Table 16.3 and discuss the differences.
-means converge?
Compare the result with the EM clustering
in Table 16.3 and discuss the differences.
- Modify the expectation and maximization steps of EM
for a Gaussian mixture. The
maximization step computes the maximum likelihood parameter
estimates
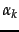 ,
, 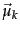 , and
, and 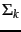 for each
of the clusters. The expectation step computes for each
vector a soft assignment to clusters (Gaussians) based on their current
parameters.
Write down the equations for Gaussian mixtures corresponding to
and 202 .
for each
of the clusters. The expectation step computes for each
vector a soft assignment to clusters (Gaussians) based on their current
parameters.
Write down the equations for Gaussian mixtures corresponding to
and 202 .
- Show that
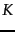 -means can be viewed as the limiting case
of
EM for Gaussian mixtures if variance is very small and all
covariances are 0.
-means can be viewed as the limiting case
of
EM for Gaussian mixtures if variance is very small and all
covariances are 0.
- The within-point scatter of a clustering
is
defined as
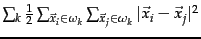 .
Show that minimizing RSS and minimizing within-point scatter
are equivalent.
.
Show that minimizing RSS and minimizing within-point scatter
are equivalent.
- Derive an AIC criterion
for the multivariate Bernoulli
mixture model
from Equation 196.





Next: Hierarchical clustering
Up: Flat clustering
Previous: References and further reading
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07