Model-based clustering

In this section, we describe a generalization of $K$-means, the EM algorithm. It can be applied to a larger variety of document representations and distributions than $K$-means.

In $K$-means, we attempt to find centroids that are good representatives. We can view the set of $K$ centroids as a model that generates the data. Generating a document in this model consists of first picking a centroid at random and then adding some noise. If the noise is normally distributed, this procedure will result in clusters of spherical shape. Model-based clustering assumes that the data were generated by a model and tries to recover the original model from the data. The model that we recover from the data then defines clusters and an assignment of documents to clusters.

A commonly used criterion for estimating the model parameters is maximum likelihood. In $K$-means, the quantity $\exp(-\mbox{RSS})$ is proportional to the likelihood that a particular model (i.e., a set of centroids) generated the data. For $K$-means, maximum likelihood and minimal RSS are equivalent criteria. We denote the model parameters by $\Theta$. In $K$-means, $\Theta = \{ \vec{\mu}_1, \ldots ,\vec{\mu}_K \}$.

More generally, the maximum likelihood criterion is to select the parameters $\Theta$ that maximize the log-likelihood of generating the data $D$:

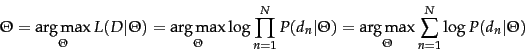$$\Theta = \argmax_{\Theta} L(D\vert\Theta) = \argmax_{\Theta... ...heta) = \argmax_{\Theta} \sum_{n=1}^N \log P(d_n\vert \Theta)$$ (198)

$L(D\vert\Theta)$ is the objective function that measures the goodness of the clustering. Given two clusterings with the same number of clusters, we prefer the one with higher $L(D\vert\Theta)$.

This is the same approach we took in Chapter 12 (page 12.1.1 ) for language modeling and in Section 13.1 (page 13.4 ) for text classification. In text classification, we chose the class that maximizes the likelihood of generating a particular document. Here, we choose the clustering $\Theta$ that maximizes the likelihood of generating a given set of documents. Once we have $\Theta$, we can compute an assignment probability $P(d\vert\omega_k;\Theta)$ for each document-cluster pair. This set of assignment probabilities defines a soft clustering.

An example of a soft assignment is that a document about Chinese cars may have a fractional membership of 0.5 in each of the two clusters China and automobiles, reflecting the fact that both topics are pertinent. A hard clustering like $K$-means cannot model this simultaneous relevance to two topics.

Model-based clustering provides a framework for incorporating our knowledge about a domain. $K$-means and the hierarchical algorithms in Chapter 17 make fairly rigid assumptions about the data. For example, clusters in $K$-means are assumed to be spheres. Model-based clustering offers more flexibility. The clustering model can be adapted to what we know about the underlying distribution of the data, be it Bernoulli (as in the example in Table 16.3 ), Gaussian with non-spherical variance (another model that is important in document clustering) or a member of a different family.

A commonly used algorithm for model-based clustering is the Expectation-Maximization algorithm or EM algorithm . EM clustering is an iterative algorithm that maximizes $L(D\vert\Theta)$. EM can be applied to many different types of probabilistic modeling. We will work with a mixture of multivariate Bernoulli distributions here, the distribution we know from Section 11.3 (page 11.3 ) and Section 13.3 (page 13.3 ):

$$P(d\vert \omega_k ; \Theta) = \left( \prod_{\tcword_m \in d} q_{mk} \right) \left( \prod_{\tcword_m \notin d} (1-q_{mk}) \right)$$ (199)

where $\Theta = \{ \Theta_1,\ldots,\Theta_K \}$, $\Theta_k = (\alpha_k , q_{1k}, \ldots, q_{Mk})$, and $q_{mk} = P(\wvar_m=1 \vert \omega_k)$ are the parameters of the model. $P(\wvar_m=1\vert\omega_k)$ is the probability that a document from cluster $\omega_k$ contains term $\tcword_m$. The probability $\alpha_k$ is the prior of cluster $\omega_k$: the probability that a document $d$ is in $\omega_k$ if we have no information about $d$.

The mixture model then is:

$$P(d\vert \Theta) = \sum_{k=1}^{K} \alpha_k \left( \prod_{\tcword_m \in d} q_{mk} \right) \left( \prod_{\tcword_m \notin d} (1-q_{mk}) \right)$$ (200)

In this model, we generate a document by first picking a cluster $k$ with probability $\alpha_k$ and then generating the terms of the document according to the parameters $q_{mk}$. Recall that the document representation of the multivariate Bernoulli is a vector of $M$ Boolean values (and not a real-valued vector).

How do we use EM to infer the parameters of the clustering from the data? That is, how do we choose parameters $\Theta$ that maximize $L(D\vert\Theta)$? EM is similar to $K$-means in that it alternates between an expectation step , corresponding to reassignment, and a maximization step , corresponding to recomputation of the parameters of the model. The parameters of $K$-means are the centroids, the parameters of the instance of EM in this section are the $\alpha_k$ and $q_{mk}$.

The maximization step recomputes the conditional parameters $q_{mk}$ and the priors $\alpha_k$ as follows:

$$\mbox{\bf Maximization step:} \quad q_{mk} = \frac{\sum_{n=1}^N r... ...\in d_n )} {\sum_{n=1}^N r_{nk}} \quad \alpha_k = \frac{\sum_{n=1}^N r_{nk}}{N}$$ (201)

where $I( \tcword_m \in d_n )=1$ if $\tcword_m \in d_n$ and 0 otherwise and $r_{nk}$ is the soft assignment of document $d_n$ to cluster $k$ as computed in the preceding iteration. (We'll address the issue of initialization in a moment.) These are the maximum likelihood estimates for the parameters of the multivariate Bernoulli from Table 13.3 (page 13.3 ) except that documents are assigned fractionally to clusters here. These maximum likelihood estimates maximize the likelihood of the data given the model.

The expectation step computes the soft assignment of documents to clusters given the current parameters $q_{mk}$ and $\alpha_k$:

$${\bf Expectation \ step:} \quad r_{nk} = \frac{ \alpha_k (\prod_{... ... (\prod_{\tcword_m \in d_n} q_{mk}) (\prod_{\tcword_m \notin d_n} (1-q_{mk})) }$$ (202)

This expectation step applies and 200 to computing the likelihood that $\omega_k$ generated document $d_n$. It is the classification procedure for the multivariate Bernoulli in Table 13.3 . Thus, the expectation step is nothing else but Bernoulli Naive Bayes classification (including normalization, i.e. dividing by the denominator, to get a probability distribution over clusters).

(a)	docID	document text	docID	document text
	1	hot chocolate cocoa beans	7	sweet sugar
	2	cocoa ghana africa	8	sugar cane brazil
	3	beans harvest ghana	9	sweet sugar beet
	4	cocoa butter	10	sweet cake icing
	5	butter truffles	11	cake black forest
	6	sweet chocolate

(b)	Parameter	Iteration of clustering
		0	1	2	3	4	5	15	25
	$\alpha_1$		0.50	0.45	0.53	0.57	0.58	0.54	0.45
	$r_{1,1}$		1.00	1.00	1.00	1.00	1.00	1.00	1.00
	$r_{2,1}$		0.50	0.79	0.99	1.00	1.00	1.00	1.00
	$r_{3,1}$		0.50	0.84	1.00	1.00	1.00	1.00	1.00
	$r_{4,1}$		0.50	0.75	0.94	1.00	1.00	1.00	1.00
	$r_{5,1}$		0.50	0.52	0.66	0.91	1.00	1.00	1.00
	$r_{6,1}$	1.00	1.00	1.00	1.00	1.00	1.00	0.83	0.00
	$r_{7,1}$	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	$r_{8,1}$		0.00	0.00	0.00	0.00	0.00	0.00	0.00
	$r_{9,1}$		0.00	0.00	0.00	0.00	0.00	0.00	0.00
	$r_{10,1}$		0.50	0.40	0.14	0.01	0.00	0.00	0.00
	$r_{11,1}$		0.50	0.57	0.58	0.41	0.07	0.00	0.00
	$q_{africa,1}$		0.000	0.100	0.134	0.158	0.158	0.169	0.200
	$q_{africa,2}$		0.000	0.083	0.042	0.001	0.000	0.000	0.000
	$q_{brazil,1}$		0.000	0.000	0.000	0.000	0.000	0.000	0.000
	$q_{brazil,2}$		0.000	0.167	0.195	0.213	0.214	0.196	0.167
	$q_{cocoa,1}$		0.000	0.400	0.432	0.465	0.474	0.508	0.600
	$q_{cocoa,2}$		0.000	0.167	0.090	0.014	0.001	0.000	0.000
	$q_{sugar,1}$		0.000	0.000	0.000	0.000	0.000	0.000	0.000
	$q_{sugar,2}$		1.000	0.500	0.585	0.640	0.642	0.589	0.500
	$q_{sweet,1}$		1.000	0.300	0.238	0.180	0.159	0.153	0.000
	$q_{sweet,2}$		1.000	0.417	0.507	0.610	0.640	0.608	0.667

The EM clustering algorithm.The table shows a set of documents (a) and parameter values for selected iterations during EM clustering (b). Parameters shown are prior $\alpha_1$, soft assignment scores $r_{n,1}$ (both omitted for cluster 2), and lexical parameters $q_{m,k}$ for a few terms. The authors initially assigned document 6 to cluster 1 and document 7 to cluster 2 (iteration 0). EM converges after 25 iterations. For smoothing, the $r_{nk}$ in Equation 201 were replaced with $r_{nk}+\epsilon$ where $\epsilon = 0.0001$.

We clustered a set of 11 documents into two clusters using EM in Table 16.3 . After convergence in iteration 25, the first 5 documents are assigned to cluster 1 ( $r_{i,1} = 1.00$) and the last 6 to cluster 2 ($r_{i,1}=0.00$). Somewhat atypically, the final assignment is a hard assignment here. EM usually converges to a soft assignment. In iteration 25, the prior $\alpha_1$ for cluster 1 is $5/11 \approx 0.45$ because 5 of the 11 documents are in cluster 1. Some terms are quickly associated with one cluster because the initial assignment can ``spread'' to them unambiguously. For example, membership in cluster 2 spreads from document 7 to document 8 in the first iteration because they share sugar ($r_{8,1}=0$ in iteration 1).

For parameters of terms occurring in ambiguous contexts, convergence takes longer. Seed documents 6 and 7 both contain sweet. As a result, it takes 25 iterations for the term to be unambiguously associated with cluster 2. ($q_{sweet,1}=0$ in iteration 25.)

Finding good seeds is even more critical for EM than for $K$-means. EM is prone to get stuck in local optima if the seeds are not chosen well. This is a general problem that also occurs in other applications of EM.Therefore, as with $K$-means, the initial assignment of documents to clusters is often computed by a different algorithm. For example, a hard $K$-means clustering may provide the initial assignment, which EM can then ``soften up.''

Exercises.

• We saw above that the time complexity of $K$-means is $\Theta(IKNM)$. What is the time complexity of EM?