




Next: Types of language models
Up: Language models
Previous: Language models
Contents
Index
What do we mean by a document model generating a query? A traditional
generative model of a language, of the kind familiar from formal
language theory, can be used either to recognize or to generate strings.
For example, the finite automaton shown in Figure 12.1 can generate
strings that include the examples shown. The full set of strings that
can be generated is called the language of the
automaton.![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png)
If instead each node has a probability distribution over generating
different terms, we have a language model. The notion of a language model is inherently probabilistic. A language model
is a function that puts a
probability measure over strings drawn from some vocabulary. That is, for
a language model 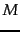 over an alphabet
over an alphabet 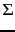 :
:
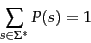 |
(90) |
One simple kind of language model is equivalent to a probabilistic
finite automaton consisting of just a single node
with a single probability distribution over producing different terms,
so that
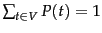 , as
shown in Figure 12.2 . After generating each word, we decide whether
to stop or to loop around and then produce another word, and so the
model also requires a probability of stopping in the
finishing state. Such a model places a probability distribution
over any sequence of words. By construction, it also provides a model
for generating text according to its distribution.
, as
shown in Figure 12.2 . After generating each word, we decide whether
to stop or to loop around and then produce another word, and so the
model also requires a probability of stopping in the
finishing state. Such a model places a probability distribution
over any sequence of words. By construction, it also provides a model
for generating text according to its distribution.
Worked example. To find the
probability of a word sequence, we just multiply the probabilities
which the model gives to each word in the sequence, together with the
probability of continuing or stopping after producing each word. For example,
As you can see, the probability of a particular string/document, is usually a
very small number! Here we stopped after generating frog the
second time. The
first line of numbers are the term emission probabilities, and the
second line gives the probability of continuing or stopping after
generating each word. An explicit
stop probability is needed for a finite automaton to be a well-formed
language model according to Equation 90. Nevertheless, most
of the time, we will omit to include STOP and
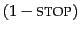 probabilities (as do most
other authors). To compare two models for a data set, we can
calculate their likelihood ratio , which results from simply dividing
the probability of the data according to one model by the probability
of the data according to the other model.
Providing that the stop probability is
fixed, its inclusion will not alter the likelihood ratio that results
from comparing the likelihood of two language models generating
a string. Hence, it will not alter the ranking of documents.
probabilities (as do most
other authors). To compare two models for a data set, we can
calculate their likelihood ratio , which results from simply dividing
the probability of the data according to one model by the probability
of the data according to the other model.
Providing that the stop probability is
fixed, its inclusion will not alter the likelihood ratio that results
from comparing the likelihood of two language models generating
a string. Hence, it will not alter the ranking of documents.![[*]](http://nlp.stanford.edu/IR-book/html/icons/footnote.png) Nevertheless, formally, the numbers will no longer truly be
probabilities, but only proportional to probabilities. See
Exercise 12.1.3 .
End worked example.
Nevertheless, formally, the numbers will no longer truly be
probabilities, but only proportional to probabilities. See
Exercise 12.1.3 .
End worked example.
Figure 12.3:
Partial specification of two unigram language
models.
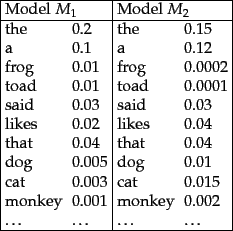 |
Worked example. Suppose, now, that we have two language models 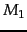 and
and 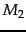 , shown
partially in Figure 12.3 . Each gives a probability estimate to a
sequence of terms, as already illustrated in m1probability.
The language model that
gives the higher probability to the sequence of terms is more likely to
have generated the term sequence. This time, we will omit
STOP probabilities from our calculations.
For the sequence shown, we get:
, shown
partially in Figure 12.3 . Each gives a probability estimate to a
sequence of terms, as already illustrated in m1probability.
The language model that
gives the higher probability to the sequence of terms is more likely to
have generated the term sequence. This time, we will omit
STOP probabilities from our calculations.
For the sequence shown, we get:
![\begin{example}
\begin{tabular}[t]{lllllllll}
$s$\ & frog & said & that & toad &...
...column{5}{l}{$P(s\vert M_2) = 0.000000000000000384 $}
\end{tabular}\end{example}](img805.png)
and we see that
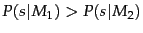 .
We present the formulas here in terms of products of probabilities,
but, as is common in probabilistic applications, in practice it is
usually best to work with sums of log probabilities (cf. page 13.2 ).
End worked example.
.
We present the formulas here in terms of products of probabilities,
but, as is common in probabilistic applications, in practice it is
usually best to work with sums of log probabilities (cf. page 13.2 ).
End worked example.





Next: Types of language models
Up: Language models
Previous: Language models
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07

![]()
![]() over an alphabet
over an alphabet ![]() :
:
![]() and
and ![]() , shown
partially in Figure 12.3 . Each gives a probability estimate to a
sequence of terms, as already illustrated in m1probability.
The language model that
gives the higher probability to the sequence of terms is more likely to
have generated the term sequence. This time, we will omit
STOP probabilities from our calculations.
For the sequence shown, we get:
, shown
partially in Figure 12.3 . Each gives a probability estimate to a
sequence of terms, as already illustrated in m1probability.
The language model that
gives the higher probability to the sequence of terms is more likely to
have generated the term sequence. This time, we will omit
STOP probabilities from our calculations.
For the sequence shown, we get:
![\begin{example}
\begin{tabular}[t]{lllllllll}
$s$\ & frog & said & that & toad &...
...column{5}{l}{$P(s\vert M_2) = 0.000000000000000384 $}
\end{tabular}\end{example}](img805.png)
![]() .
We present the formulas here in terms of products of probabilities,
but, as is common in probabilistic applications, in practice it is
usually best to work with sums of log probabilities (cf. page 13.2 ).
End worked example.
.
We present the formulas here in terms of products of probabilities,
but, as is common in probabilistic applications, in practice it is
usually best to work with sums of log probabilities (cf. page 13.2 ).
End worked example.