Types of language models

How do we build probabilities over sequences of terms? We can always use the chain rule from Equation 56 to decompose the probability of a sequence of events into the probability of each successive event conditioned on earlier events:

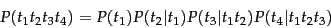$$P(t_1t_2t_3t_4) = P(t_1)P(t_2\vert t_1)P(t_3\vert t_1t_2)P(t_4\vert t_1t_2t_3)$$ (94)

The simplest form of language model simply throws away all conditioning context, and estimates each term independently. Such a model is called a unigram language model :

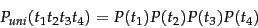$$P_{uni}(t_1t_2t_3t_4) = P(t_1)P(t_2)P(t_3)P(t_4)$$ (95)

There are many more complex kinds of language models, such as bigram language models , which condition on the previous term,

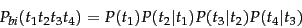$$P_{bi}(t_1t_2t_3t_4) = P(t_1)P(t_2\vert t_1)P(t_3\vert t_2)P(t_4\vert t_3)$$ (96)

and even more complex grammar-based language models such as probabilistic context-free grammars. Such models are vital for tasks like speech recognition , spelling correction , and machine translation , where you need the probability of a term conditioned on surrounding context. However, most language-modeling work in IR has used unigram language models. IR is not the place where you most immediately need complex language models, since IR does not directly depend on the structure of sentences to the extent that other tasks like speech recognition do. Unigram models are often sufficient to judge the topic of a text. Moreover, as we shall see, IR language models are frequently estimated from a single document and so it is questionable whether there is enough training data to do more. Losses from data sparseness (see the discussion on page 13.2 ) tend to outweigh any gains from richer models. This is an example of the bias-variance tradeoff (cf. secbiasvariance): With limited training data, a more constrained model tends to perform better. In addition, unigram models are more efficient to estimate and apply than higher-order models. Nevertheless, the importance of phrase and proximity queries in IR in general suggests that future work should make use of more sophisticated language models, and some has begun to lmir-refs. Indeed, making this move parallels the model of van Rijsbergen in Chapter 11 (page 11.4.2 ).