




Next: Latent semantic indexing
Up: Matrix decompositions and latent
Previous: Term-document matrices and singular
Contents
Index
Low-rank approximations
We next state a matrix approximation problem that at first seems to have little to do with information retrieval. We describe a solution to this matrix problem using singular-value decompositions, then develop its application to information retrieval.
Given an
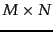 matrix
matrix 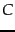 and a positive integer
and a positive integer  , we wish to find an
, we wish to find an
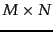 matrix
matrix 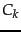 of rank at most
of rank at most  , so as to minimize the Frobenius norm of the matrix difference
, so as to minimize the Frobenius norm of the matrix difference
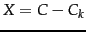 , defined to be
, defined to be
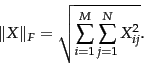 |
(238) |
Thus, the Frobenius norm of 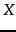 measures the discrepancy between
measures the discrepancy between 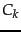 and
and 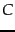 ; our goal is to find a matrix
; our goal is to find a matrix 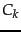 that minimizes this discrepancy, while constraining
that minimizes this discrepancy, while constraining 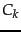 to have rank at most
to have rank at most  . If
. If 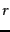 is the rank of
is the rank of 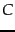 , clearly
, clearly
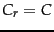 and the Frobenius norm of the discrepancy is zero in this case. When
and the Frobenius norm of the discrepancy is zero in this case. When  is far smaller than
is far smaller than 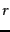 , we refer to
, we refer to 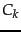 as a low-rank approximation .
as a low-rank approximation .
The singular value decomposition can be used to solve the low-rank matrix approximation problem. We then derive from it an application to approximating term-document matrices. We invoke the following three-step procedure to this end:
- Given
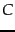 , construct its SVD in the form shown in (232); thus,
, construct its SVD in the form shown in (232); thus,
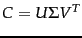 .
.
- Derive from
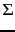 the matrix
the matrix 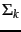 formed by replacing by zeros the
formed by replacing by zeros the 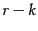 smallest singular values on the diagonal of
smallest singular values on the diagonal of 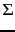 .
.
- Compute and output
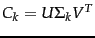 as the rank-
as the rank- approximation to
approximation to 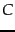 .
.
The rank of 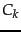 is at most
is at most  : this follows from the fact that
: this follows from the fact that 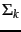 has at most
has at most  non-zero values. Next, we recall the intuition of Example 18.1: the effect of small eigenvalues on matrix products is small. Thus, it seems plausible that replacing these small eigenvalues by zero will not substantially alter the product, leaving it ``close'' to
non-zero values. Next, we recall the intuition of Example 18.1: the effect of small eigenvalues on matrix products is small. Thus, it seems plausible that replacing these small eigenvalues by zero will not substantially alter the product, leaving it ``close'' to 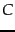 . The following theorem due to Eckart and Young tells us that, in fact, this procedure yields the matrix of rank
. The following theorem due to Eckart and Young tells us that, in fact, this procedure yields the matrix of rank  with the lowest possible Frobenius error.
with the lowest possible Frobenius error.
Theorem.
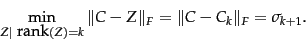 |
(239) |
End theorem.
Recalling that the singular values are in decreasing order
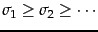 , we learn from
Theorem 18.3 that
, we learn from
Theorem 18.3 that 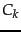 is the best
rank-
is the best
rank- approximation to
approximation to 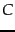 , incurring an error (measured
by the Frobenius norm of
, incurring an error (measured
by the Frobenius norm of
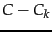 ) equal to
) equal to 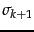 .
Thus the larger
.
Thus the larger  is, the smaller this error (and in particular, for
is, the smaller this error (and in particular, for 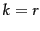 , the error is zero since
, the error is zero since
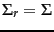 ; provided
; provided 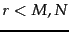 , then
, then
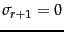 and thus
and thus
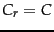 ).
).
To derive further insight into why the process of truncating the smallest 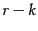 singular values in
singular values in 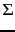 helps generate a rank-
helps generate a rank- approximation of low error, we examine the form of
approximation of low error, we examine the form of 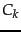 :
:
where 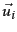 and
and 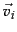 are the
are the 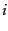 th columns of
th columns of 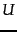 and
and 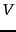 , respectively. Thus,
, respectively. Thus,
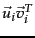 is a rank-1 matrix, so that we have just expressed
is a rank-1 matrix, so that we have just expressed 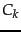 as the sum of
as the sum of  rank-1 matrices each weighted by a singular value. As
rank-1 matrices each weighted by a singular value. As 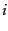 increases, the contribution of the rank-1 matrix
increases, the contribution of the rank-1 matrix
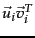 is weighted by a sequence of shrinking singular values
is weighted by a sequence of shrinking singular values 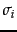 .
.
Exercises.





Next: Latent semantic indexing
Up: Matrix decompositions and latent
Previous: Term-document matrices and singular
Contents
Index
© 2008 Cambridge University Press
This is an automatically generated page. In case of formatting errors you may want to look at the PDF edition of the book.
2009-04-07
![]() matrix
matrix ![]() and a positive integer
and a positive integer ![]() , we wish to find an
, we wish to find an
![]() matrix
matrix ![]() of rank at most
of rank at most ![]() , so as to minimize the Frobenius norm of the matrix difference
, so as to minimize the Frobenius norm of the matrix difference
![]() , defined to be
, defined to be
![]() , we learn from
Theorem 18.3 that
, we learn from
Theorem 18.3 that ![]() is the best
rank-
is the best
rank-![]() approximation to
approximation to ![]() , incurring an error (measured
by the Frobenius norm of
, incurring an error (measured
by the Frobenius norm of
![]() ) equal to
) equal to ![]() .
Thus the larger
.
Thus the larger ![]() is, the smaller this error (and in particular, for
is, the smaller this error (and in particular, for ![]() , the error is zero since
, the error is zero since
![]() ; provided
; provided ![]() , then
, then
![]() and thus
and thus
![]() ).
).
![]() singular values in
singular values in ![]() helps generate a rank-
helps generate a rank-![]() approximation of low error, we examine the form of
approximation of low error, we examine the form of ![]() :
:
![]() in Example 18.2, write down both
in Example 18.2, write down both ![]() and
and ![]() .
.