Another popular feature selection
method is ![]() .
In statistics, the
.
In statistics, the ![]() test is
applied to test the independence of two events,
where two events A and B are defined to be
independent if
test is
applied to test the independence of two events,
where two events A and B are defined to be
independent if
![]() or, equivalently,
or, equivalently,
![]() and
and
![]() . In
feature selection, the two events are occurrence of the
term and occurrence of the class.
We then rank terms with respect to the following
quantity:
. In
feature selection, the two events are occurrence of the
term and occurrence of the class.
We then rank terms with respect to the following
quantity:
Worked example. We first
compute ![]() for the
data in Example 13.5.1:
for the
data in Example 13.5.1:
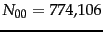 |
(134) | ||
 |
(135) |
We compute the other
![]() in the same way:
in the same way:
Plugging these values into
Equation 133, we get a ![]() value of 284:
value of 284:
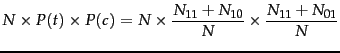 |
(136) |
| 0.1 | 2.71 |
| 0.05 | 3.84 |
| 0.01 | 6.63 |
| 0.005 | 7.88 |
| 0.001 | 10.83 |
![]() is a measure of how much expected counts
is a measure of how much expected counts ![]() and observed
counts
and observed
counts ![]() deviate from each other. A high value of
deviate from each other. A high value of ![]() indicates that the hypothesis of independence, which implies
that expected and observed counts are similar, is
incorrect. In our example,
indicates that the hypothesis of independence, which implies
that expected and observed counts are similar, is
incorrect. In our example,
![]() . Based
on Table 13.6 , we can reject the hypothesis that
poultry and export are independent with only
a 0.001 chance of being wrong.
. Based
on Table 13.6 , we can reject the hypothesis that
poultry and export are independent with only
a 0.001 chance of being wrong.![]() Equivalently, we say that the outcome
Equivalently, we say that the outcome
![]() is statistically
significant at the 0.001 level. If the two events are
dependent, then the occurrence of the term makes the occurrence
of the class more likely (or less likely), so it should be
helpful as a feature. This is the rationale of
is statistically
significant at the 0.001 level. If the two events are
dependent, then the occurrence of the term makes the occurrence
of the class more likely (or less likely), so it should be
helpful as a feature. This is the rationale of ![]() feature selection.
feature selection.
An arithmetically simpler way of computing ![]() is the
following:
is the
following: