Support vector machines: The linearly separable case

Figure 15.1: The support vectors are the 5 points right up against the margin of the classifier.

For two-class, separable training data sets, such as the one in Figure 14.8 (page ), there are lots of possible linear separators. Intuitively, a decision boundary drawn in the middle of the void between data items of the two classes seems better than one which approaches very close to examples of one or both classes. While some learning methods such as the perceptron algorithm (see references in vclassfurther) find just any linear separator, others, like Naive Bayes, search for the best linear separator according to some criterion. The SVM in particular defines the criterion to be looking for a decision surface that is maximally far away from any data point. This distance from the decision surface to the closest data point determines the margin of the classifier. This method of construction necessarily means that the decision function for an SVM is fully specified by a (usually small) subset of the data which defines the position of the separator. 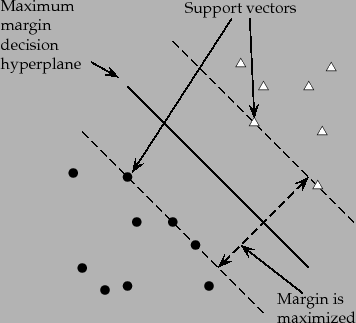These points are referred to as the support vectors (in a vector space, a point can be thought of as a vector between the origin and that point). Figure 15.1 shows the margin and support vectors for a sample problem. Other data points play no part in determining the decision surface that is chosen.

An intuition for large-margin classification.Insisting on a large margin reduces the capacity of the model: the range of angles at which the fat decision surface can be placed is smaller than for a decision hyperplane (cf. vclassline).

Maximizing the margin seems good because points near the decision surface represent very uncertain classification decisions: there is almost a 50% chance of the classifier deciding either way. A classifier with a large margin makes no low certainty classification decisions. This gives you a classification safety margin: a slight error in measurement or a slight document variation will not cause a misclassification. Another intuition motivating SVMs is shown in Figure 15.2 . By construction, an SVM classifier insists on a large margin around the decision boundary. Compared to a decision hyperplane, if you have to place a fat separator between classes, you have fewer choices of where it can be put. As a result of this, the memory capacity of the model has been decreased, and hence we expect that its ability to correctly generalize to test data is increased (cf. the discussion of the bias-variance tradeoff in Chapter 14 , page 14.6 ).

Let us formalize an SVM with algebra. A decision hyperplane (page 14.4 ) can be defined by an intercept term $b$ and a decision hyperplane normal vector $\vec{w}$ which is perpendicular to the hyperplane. This vector is commonly referred to in the machine learning literature as the weight vector . To choose among all the hyperplanes that are perpendicular to the normal vector, we specify the intercept term $b$. Because the hyperplane is perpendicular to the normal vector, all points $\vec{x}$ on the hyperplane satisfy $\vec{w}^{T}\vec{x} = -b$. Now suppose that we have a set of training data points $\docsetlabeled = \{(\vec{x}_i,y_i) \}$, where each member is a pair of a point $\vec{x}_i$ and a class label $y_i$ corresponding to it.For SVMs, the two data classes are always named $+1$ and $-1$ (rather than 1 and 0), and the intercept term is always explicitly represented as $b$ (rather than being folded into the weight vector $\vec{w}$ by adding an extra always-on feature). The math works out much more cleanly if you do things this way, as we will see almost immediately in the definition of functional margin. The linear classifier is then:

$$f(\vec{x}) = \mbox{sign}(\vec{w}^{T}\vec{x} + b)$$ (165)

A value of $-1$ indicates one class, and a value of $+1$ the other class.

We are confident in the classification of a point if it is far away from the decision boundary. For a given data set and decision hyperplane, we define the functional margin of the $i^{th}$ example $\vec{x}_i$ with respect to a hyperplane $\langle\vec{w}, b\rangle$ as the quantity $y_i(\vec{w}^{T}\vec{x}_i + b)$. The functional margin of a data set with respect to a decision surface is then twice the functional margin of any of the points in the data set with minimal functional margin (the factor of 2 comes from measuring across the whole width of the margin, as in Figure 15.3 ). However, there is a problem with using this definition as is: the value is underconstrained, because we can always make the functional margin as big as we wish by simply scaling up $\vec{w}$ and $b$. For example, if we replace $\vec{w}$ by $5\vec{w}$ and $b$ by $5b$ then the functional margin $y_i(5\vec{w}^{T}\vec{x}_i + 5b)$ is five times as large. This suggests that we need to place some constraint on the size of the $\vec{w}$ vector. To get a sense of how to do that, let us look at the actual geometry.

Figure 15.3: The geometric margin of a point ($r$) and a decision boundary ($\rho$).

What is the Euclidean distance from a point $\vec{x}$ to the decision boundary? In Figure 15.3 , we denote by $r$ this distance. We know that the shortest distance between a point and a hyperplane is perpendicular to the plane, and hence, parallel to $\vec{w}$. A unit vector in this direction is $\vec{w}/\vert\vec{w}\vert$. The dotted line in the diagram is then a translation of the vector $r\vec{w}/\vert\vec{w}\vert$. Let us label the point on the hyperplane closest to $\vec{x}$ as $\vec{x}'$. Then:

$$\vec{x}' = \vec{x} - yr \frac{\vec{w}}{\vert\vec{w}\vert}$$ (166)

where multiplying by $y$ just changes the sign for the two cases of $\vec{x}$ being on either side of the decision surface. Moreover, $\vec{x}'$ lies on the decision boundary and so satisfies $\vec{w}^{T}\vec{x}' + b = 0$. Hence:

$$\vec{w}^{T}\big(\vec{x} - yr \frac{\vec{w}}{\vert\vec{w}\vert}\big) + b = 0$$ (167)

Solving for $r$ gives:

$$r = y \frac{\vec{w}^{T}\vec{x} + b}{\vert\vec{w}\vert}$$ (168)

Again, the points closest to the separating hyperplane are support vectors. The geometric margin of the classifier is the maximum width of the band that can be drawn separating the support vectors of the two classes. That is, it is twice the minimum value over data points for $r$ given in Equation 168, or, equivalently, the maximal width of one of the fat separators shown in Figure 15.2 . The geometric margin is clearly invariant to scaling of parameters: if we replace $\vec{w}$ by $5\vec{w}$ and $b$ by $5b$, then the geometric margin is the same, because it is inherently normalized by the length of $\vec{w}$. This means that we can impose any scaling constraint we wish on $\vec{w}$ without affecting the geometric margin. Among other choices, we could use unit vectors, as in Chapter 6 , by requiring that $\vert\vec{w}\vert = 1$. This would have the effect of making the geometric margin the same as the functional margin.

Since we can scale the functional margin as we please, for convenience in solving large SVMs, let us choose to require that the functional margin of all data points is at least 1 and that it is equal to 1 for at least one data vector. That is, for all items in the data:

$$y_i(\vec{w}^{T}\vec{x}_i + b) \ge 1$$ (169)

and there exist support vectors for which the inequality is an equality. Since each example's distance from the hyperplane is $r_i = y_i(\vec{w}^{T}\vec{x}_i + b)/\vert\vec{w}\vert$, the geometric margin is $\rho = 2/\vert\vec{w}\vert$. Our desire is still to maximize this geometric margin. That is, we want to find $\vec{w}$ and $b$ such that:

• $\rho = 2/\vert\vec{w}\vert$ is maximized
• For all $(\vec{x}_i, y_i) \in \docsetlabeled$, $y_i(\vec{w}^{T}\vec{x}_i + b) \ge 1$

Maximizing $2/\vert\vec{w}\vert$ is the same as minimizing $\vert\vec{w}\vert/2$. This gives the final standard formulation of an SVM as a minimization problem:

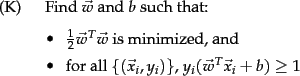
We are now optimizing a quadratic function subject to linear constraints. Quadratic optimization problems are a standard, well-known class of mathematical optimization problems, and many algorithms exist for solving them. We could in principle build our SVM using standard quadratic programming (QP) libraries, but there has been much recent research in this area aiming to exploit the structure of the kind of QP that emerges from an SVM. As a result, there are more intricate but much faster and more scalable libraries available especially for building SVMs, which almost everyone uses to build models. We will not present the details of such algorithms here.

However, it will be helpful to what follows to understand the shape of the solution of such an optimization problem. The solution involves constructing a dual problem where a Lagrange multiplier $\alpha_i$ is associated with each constraint $y_i(\vec{w}^{T}\vec{x_i} + b) \ge 1$ in the primal problem:

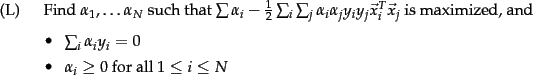
The solution is then of the form:

In the solution, most of the $\alpha_i$ are zero. Each non-zero $\alpha_i$ indicates that the corresponding $\vec{x}_i$ is a support vector. The classification function is then:

$$f(\vec{x}) = \mbox{sign}(\sum\nolimits_i \alpha_iy_i\vec{x}_i^{T}\vec{x} + b)$$ (170)

Both the term to be maximized in the dual problem and the classifying function involve a dot product between pairs of points ($\vec{x}$ and $\vec{x}_i$ or $\vec{x}_i$ and $\vec{x}_j$), and that is the only way the data are used - we will return to the significance of this later.

To recap, we start with a training data set. The data set uniquely defines the best separating hyperplane, and we feed the data through a quadratic optimization procedure to find this plane. Given a new point $\vec{x}$ to classify, the classification function $f(\vec{x})$ in either Equation 165 or Equation 170 is computing the projection of the point onto the hyperplane normal. The sign of this function determines the class to assign to the point. If the point is within the margin of the classifier (or another confidence threshold $t$ that we might have determined to minimize classification mistakes) then the classifier can return ``don't know'' rather than one of the two classes. The value of $f(\vec{x})$ may also be transformed into a probability of classification; fitting a sigmoid to transform the values is standard (Platt, 2000). Also, since the margin is constant, if the model includes dimensions from various sources, careful rescaling of some dimensions may be required. However, this is not a problem if our documents (points) are on the unit hypersphere.

Figure 15.4: A tiny 3 data point training set for an SVM.

Worked example. Consider building an SVM over the (very little) data set shown in Figure 15.4 . Working geometrically, for an example like this, the maximum margin weight vector will be parallel to the shortest line connecting points of the two classes, that is, the line between $(1,1)$ and $(2,3)$, giving a weight vector of $(1,2)$. The optimal decision surface is orthogonal to that line and intersects it at the halfway point. Therefore, it passes through $(1.5,2)$. So, the SVM decision boundary is:

$$y = x_1 + 2x_2 - 5.5$$ (171)

Working algebraically, with the standard constraint that $\mbox{sign}(y_i(\vec{w}^{T}\vec{x}_i + b)) \ge 1$, we seek to minimize $\vert\vec{w}\vert$. This happens when this constraint is satisfied with equality by the two support vectors. Further we know that the solution is $\vec{w} = (a,2a)$ for some $a$. So we have that:

$$\begin{eqnarray*} a + 2a + b &=& -1 \\ 2a + 6a + b & = & 1 \end{eqnarray*}$$

Therefore, $a = 2/5$ and $b = -11/5$. So the optimal hyperplane is given by $\vec{w} = (2/5,4/5)$ and $b = -11/5$.

The margin $\rho$ is $2/\vert\vec{w}\vert = 2/\sqrt{4/25 + 16/25} = 2/(2\sqrt{5}/5) = \sqrt{5}$. This answer can be confirmed geometrically by examining Figure 15.4 .

End worked example.

Exercises.

• What is the minimum number of support vectors that there can be for a data set (which contains instances of each class)?

• The basis of being able to use kernels in SVMs (see Section 15.2.3 ) is that the classification function can be written in the form of Equation 170 (where, for large problems, most $\alpha_i$ are 0). Show explicitly how the classification function could be written in this form for the data set from small-svm-eg. That is, write $f$ as a function where the data points appear and the only variable is $\vec{x}$.

• Install an SVM package such as SVMlight (http://svmlight.joachims.org/), and build an SVM for the data set discussed in small-svm-eg. Confirm that the program gives the same solution as the text. For SVMlight, or another package that accepts the same training data format, the training file would be:

  $+$1 1:2 2:3
  $-$1 1:2 2:0
  $-$1 1:1 2:1

  The training command for SVMlight is then:

  svm_learn -c 1 -a alphas.dat train.dat model.dat

  The -c 1 option is needed to turn off use of the slack variables that we discuss in Section 15.2.1 . Check that the norm of the weight vector agrees with what we found in small-svm-eg. Examine the file alphas.dat which contains the $\alpha_i$ values, and check that they agree with your answers in Exercise 15.1 .